I. What is Prokaryotic Cell Growth?
Funny enough, many of the processes of cells actually have some sort of mathematical component or basis behind them. This is perfectly seen in bacterial cell growth when placed in a controlled medium often seen in laboratory scenarios.
Furthermore, the simplicity of prokaryotes in both their cellular structure and processes makes it much simpler to apply a mathematical model to prokaryotic cell growth! However, still try and think of similarities which apply to eukaryotic cell growth.
This will be a relatively quick and simpler article in terms of the amount and complexity of the content! You’ll see these breather articles every now and then, so do exactly that! In fact, remind yourselves always to take breathers going through this process!
II. Modeling of Prokaryotic Cell Growth
More often than not, bacterial cells are most commonly used to illustrate prokaryotic cell growth. Let’s first cover binary fission, the actual cellular mechanism for growth before discussing the exponential growth model.
A. Binary Fission
The best way to think of binary fission is as the bacterial equivalent of mitosis, except much simpler where ultimately, the bacterium generates 2 genetically identical daughter cells.
This simply involves replicating the circular DNA chromosome and other cellular components such as ribosomes and enzymes with each daughter cell getting an even distribution.
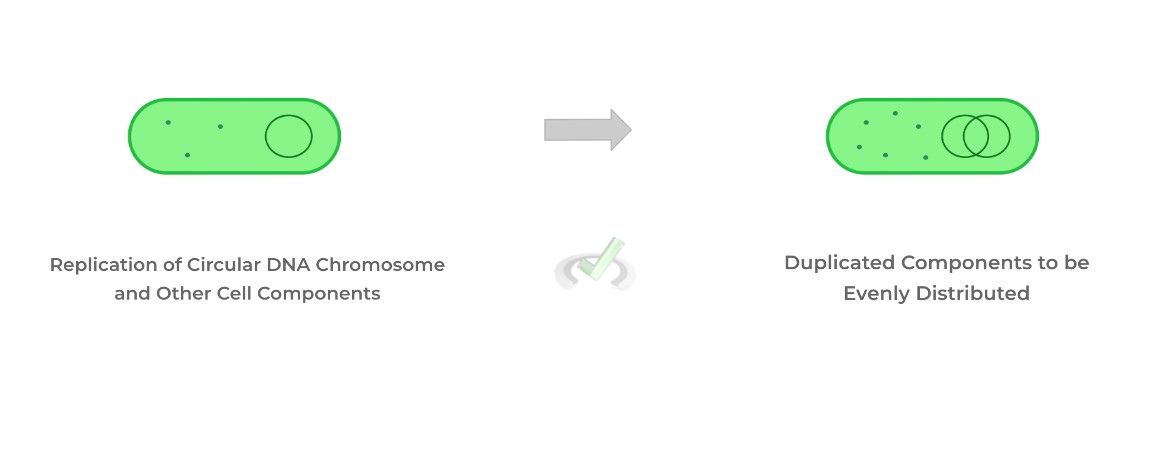
Afterwards, the cell wall and membrane start to form and invaginate the middle of the bacterium. When they come together, the 2 daughter cells are released.
Think of this as the equivalent of cytokinesis in eukaryotic cells except in this case, no cleavage furrow is used!

B. Exponential Growth Model
Notice how 1 bacterium splits into 2 daughter cells. In this way, we can model bacterial growth as an exponential function, where their growth can be modeled mathematically as shown below.
As shown in the figure above, there are 4 main phases that occur within bacterial cell growth as listed below:
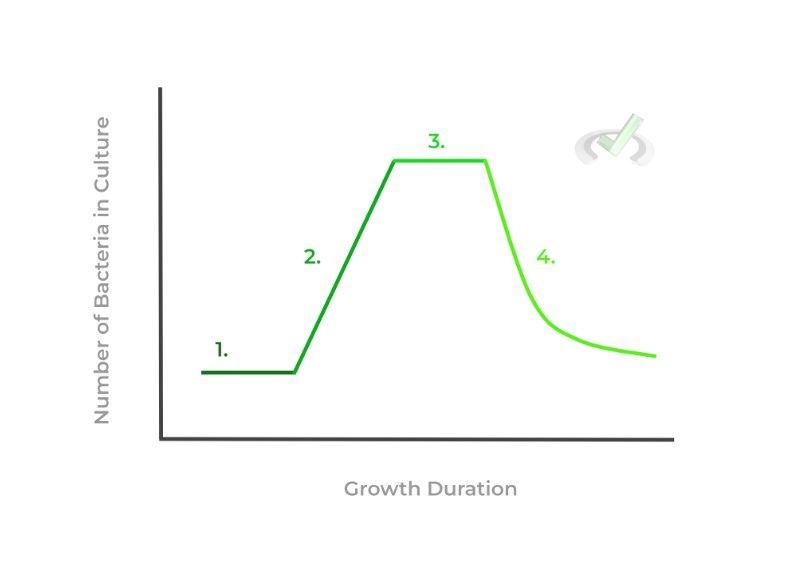
1. Lag Phase: Represents when bacteria are not yet dividing and acclimating to the new environment.
Though not yet dividing, the bacteria are readying the pathways, enzymes and substrates necessary for growth as seen in the next phase.
2. Exponential (Log) Phase: Represents stage of rapid, exponential bacterial cell growth.
This can also be modeled by an equation, where the rate of cell growth is much greater than the rate of cell death!

3. Stationary Phase: Represents the slowing of reproduction due to the depletion of nutrients and/or resources.
Here, the population that the environment can support is maximal, termed the carrying capacity.
Again, this can be modeled by an equation, where the rate of cell growth is equal to the rate of cell death!

4. Death (Decay) Phase: Represents bacterial death due to the environment no longer being able to support cell growth.
Here, the equation can be modeled where the rate of cell death is greater than the rate of cell growth!

III. Bridge/Overlap
While you won’t be required to calculate compound interest rates or calculus equations, knowing at least the basics of exponential growth won’t just be beneficial for your understanding, but also in solving problems!
1. Basics of Exponential Growth in Bacterial Cell Growth
Given its name, we’re dealing with a growth where the amount of cells increases by some exponent. We don’t want to give you any equations more complex than what’s needed, so we’ll keep it simple!
A basic equation to model bacterial cell growth is given below, where y represents the number of bacteria and x represents the number of binary fission rounds.
Hopefully, the figure below can give you a better visual of this equation when put beside the calculations!
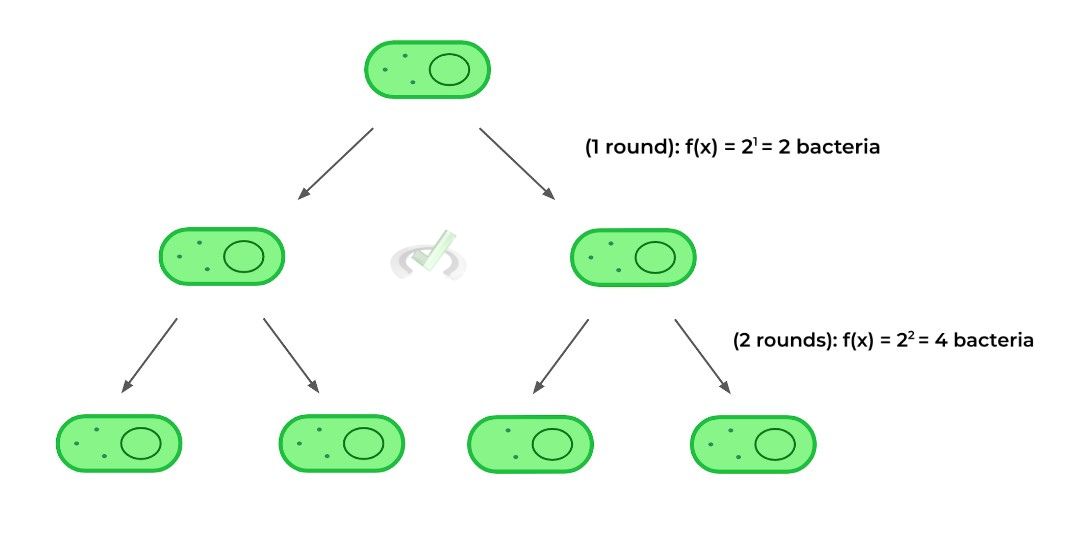
IV. Wrap Up/Key Terms
Let’s take this time to wrap up & concisely summarize what we covered above in the article!
A. Binary Fission
Essentially the prokaryotic equivalent of mitosis, binary fission allows for a bacterial cell to split into 2 genetically identical daughter cells.
After the cell has replicated the circular DNA chromosome and other cellular components, the cell wall and membrane invaginate the bacterium midline.
Once formed, the replicated circular DNA chromosome and cellular components are evenly distributed to the daughter cells.B. Exponential Growth Model
Because a bacterium can split into 2 daughter cells, bacterial growth can be mathematically modeled as an exponential function, with 4 main phases:

V. Practice
Take a look at these practice questions to see and solidify your understanding!
Sample Practice Question 1:
Starting with 1 bacterium, what will be the new bacterial population after 4 rounds of binary fission?
A. 8
B. 20
C. 16
D. 10
Ans. C
This just models a simple exponential function!If you feel that it’s better to draw a visual diagram, by all means do it! In the visual example below, consider each arrow as 1 round of replication!
1 bacteria ⇒ 2 bacteria ⇒ 4 bacteria ⇒ 8 bacteria ⇒ 16 bacteria!
Sample Practice Question 2:
When the bacterium's circular chromosome is being replicated, which phase of the cell cycle is analogous to this step?
A. G1
B. S
C. G2
D. M
Ans. B
Remember to always make connections and try to identify similarities to make learning and understanding much simpler! Recall that in the S phase of a eukaryotic cell cycle, the DNA is also replicating similar to the replication of the circular chromosome.



 To help you achieve your goal MCAT score, we take turns hosting these
To help you achieve your goal MCAT score, we take turns hosting these