Aside from the quality preparation and practice, the next best advice we can give you all for your MCAT prep is to always drink and store up on your fluids! It’s something our moms would always say when we were kids, but now being grown up, we definitely know what she meant now (thanks mom!).
When looking at the human body as a whole, it’s no surprise why we study at least the basics of fluid physics! Obviously, the most common example of fluid in the body is blood, but there are many more important fluids such as filtrate, urine, etc.
This chapter overview will cover the basics of fluid physics including the fundamental characteristics of fluids and the basic laws that guide fluid dynamics!
Fluids on the MCAT: What You Need to Know
Topics on fluids will be tested on the Chem/Phys section of the MCAT and can appear both as passage based and fundamental discrete questions.
Similar to fluids and circuits, lights and optics are some of the topics that may have a bit more emphasis on the MCAT – try and expect around 7-9 questions that cover these topics.
Introductory physics accounts for 25% of the content covered in the Chemical and Physical Foundations of Biological Systems.
Important Sub-Topics: Fluids
As mentioned above, fluid dynamics is one of the more high yield sections on the MCAT! Similar to light and optics, there are a lot of different equations and laws to memorize!
Similar to the tip we gave in our light and optics chapter overview, we suggest trying to try and make a cheat or quick sheet when you go over these different laws and equations: write the equation or law, the significance of it, and an example calculation or visual to help further explain the topic!
1. The Nature of Fluids
Simply put, fluids describe substances whose particles are able to move freely which allows them to conform to any shape of a container when placed into one. Fluids tested on the MCAT include liquids and gasses as they fit under this definition!
An important characteristic when talking about fluids is their density (𝞺), which is defined as the ratio of a fluid’s mass and its volume. This is such an important concept when discussing other physics topics such as Archimedes' principle, buoyant forces, etc., which we’ll get into!
An important application of density in fluid physics is when determining the specific gravity, which is basically a number that can be used to compare an object’s density to the density of a reference fluid, usually water as its density in the standard condition is 1 g/mL.
The concept of specific gravity is another way of putting a common concept in numerical form: if the specific gravity is less than or equal to 1 (i.e. the object is less dense or has the same density), then the object will float. If the specific gravity is greater than 1 (i.e. the object is more dense), the object will sink.
Another important characteristic and feature of liquid fluids are cohesion and adhesion which are a result of the intermolecular forces between fluid molecules! Cohesion results from the intermolecular interactions on the surface of the fluid which causes it to resist tension when applied, a phenomenon called surface tension.
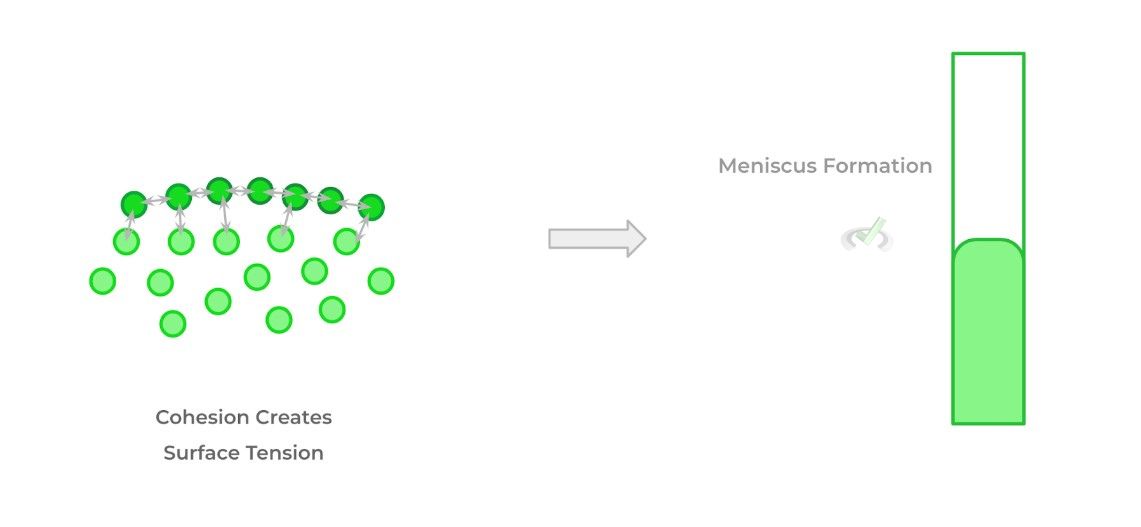
Notice how when placed in the cylinder, the fluid forms a meniscus where the edges of the fluid form downwards. This is due to the cohesion of the molecules at the surface: the surface molecules have strong inwards and downward attractions which causes the shape.
Adhesion also results from intermolecular interactions – we’ll use water as an example! The dipole moment in water confers its polarity; the polar water molecules also interact with the polar glass molecules of the cylinder which allows it to “crawl” up, also creating a meniscus but in the opposite direction!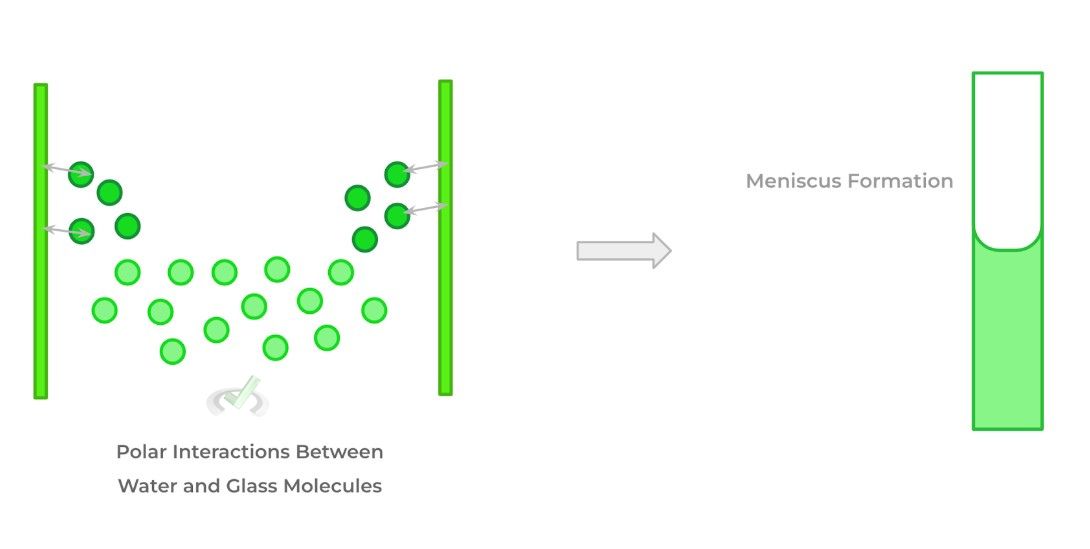
(Coming Soon!) Full Study Notes : The Nature of Fluids
For more in-depth content review on the nature of fluids, check out these detailed lesson notes created by top MCAT scorers.
2. Fluid Laws, Equations, and Effects
One important principle we’ll briefly cover is Archimedes’ principle – you’ve probably heard it accompanied by a story of Archimedes getting in a bathtub and discovering how to solve his crown problem when he realized that he displaced the bath water.
This is a great start to understanding the principle, but a more formal way to understand this is the competition between the opposing buoyant and gravitational force on an object when placed into the fluid. The buoyant force is simply the upward applied force by a fluid on a submerged object.
When an object is submerged in a fluid, it displaces a certain volume of that fluid just like when Archimedes displaced his bath water. The mass of the displaced fluid multiplied by the gravity acceleration constant will equal the buoyant force, with a vector pointing upwards against the submerged object!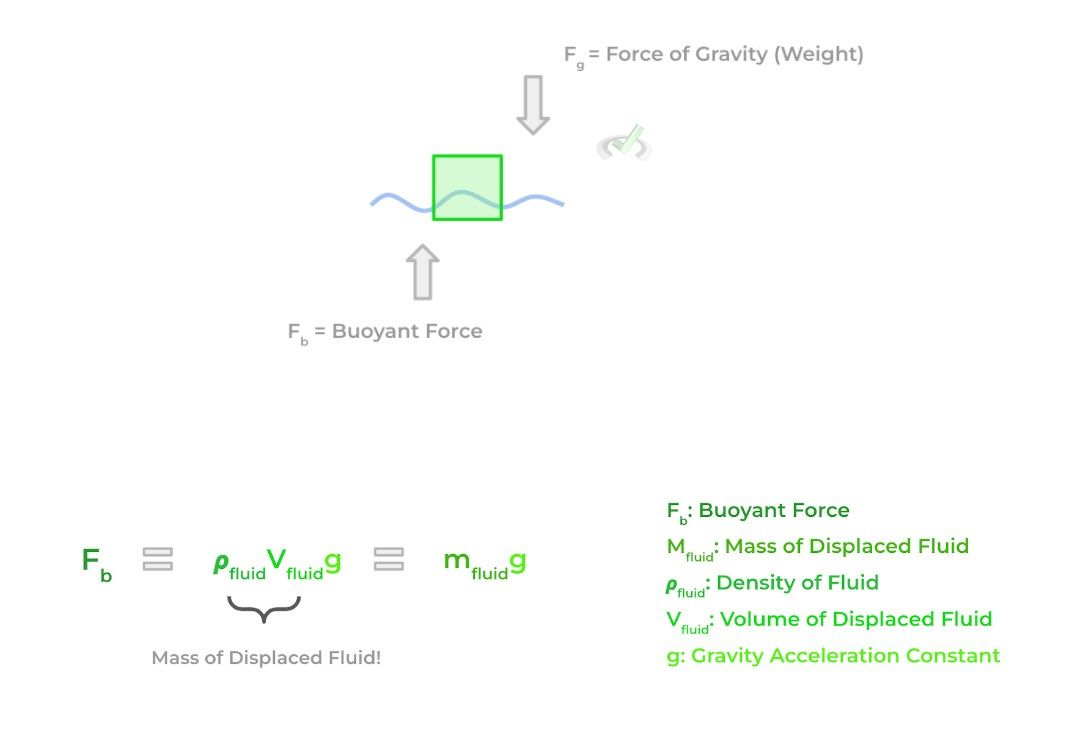
An important concept to understand is that the volume of the object that’s submerged is equal to the volume of fluid that is displaced! For example, if 3 cm3 of an object is submerged in water, then the amount of fluid displaced is also 3 cm3!
Then by knowing the density of the fluid, you can find the mass of the fluid displaced and then calculate the buoyant force! In addition, this is where we can use the concept of specific gravity to our advantage!
Recall that the specific gravity is the ratio of one substance’s density and a reference density, usually water. A trick we can use to find the volume of the substance submerged (and thus the volume of fluid displaced) is via specific gravity!
The value of the specific gravity of an object is the percentage of the object that’s submerged. For example, if an object’s specific gravity is 0.8 and has a total volume of 10 cm3, then the amount of the object submerged when placed in water is 8 cm3.
Objects with specific gravity values less than or equal to 1 (if water is the reference fluid) will float and have a buoyant force equal to their weight. Conversely, objects with specific gravity values greater than 1 will sink as the buoyant force is less than their weight.
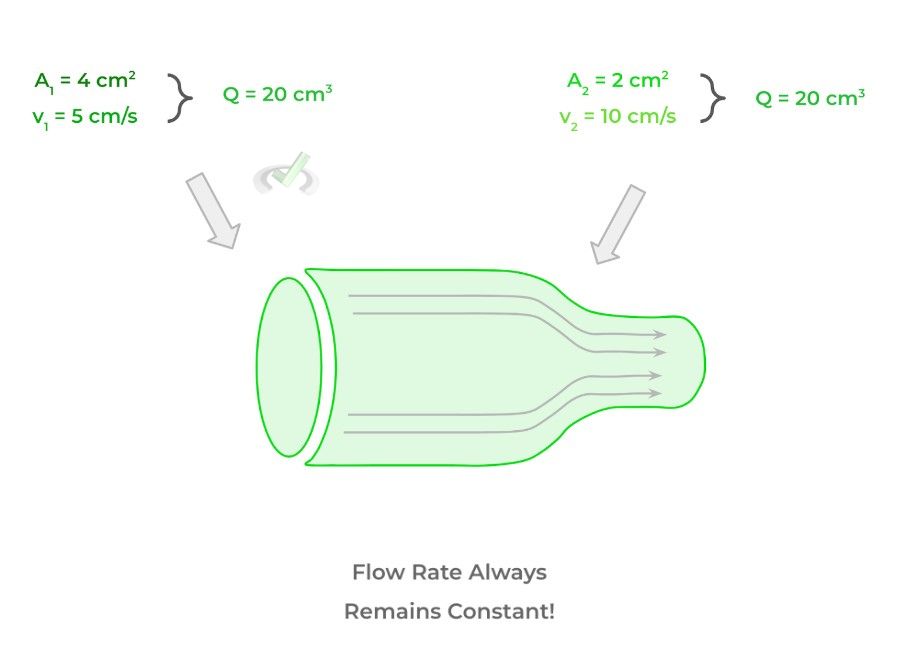
Another equation we’ll introduce in this section is the continuity equation which states that there’s an inversely proportional relationship between the tube’s cross-sectional area and the velocity of a fluid that flows in a tube or pipe!
In other words, as the cross-sectional area increases, the velocity of the fluid as it moves through the pipe decreases, and vice versa. Look at the equation below and note the similarities to other inverse proportional equations such as Boyle’s law!

Note as mentioned above that the flow rate always remains constant as this equation is basically a reiteration of the law of matter conservation. Think of it like this: if a certain amount of volume flows through one point in a given unit of time, say 3 seconds, that same amount of volume should flow through another point in 3 seconds as well!
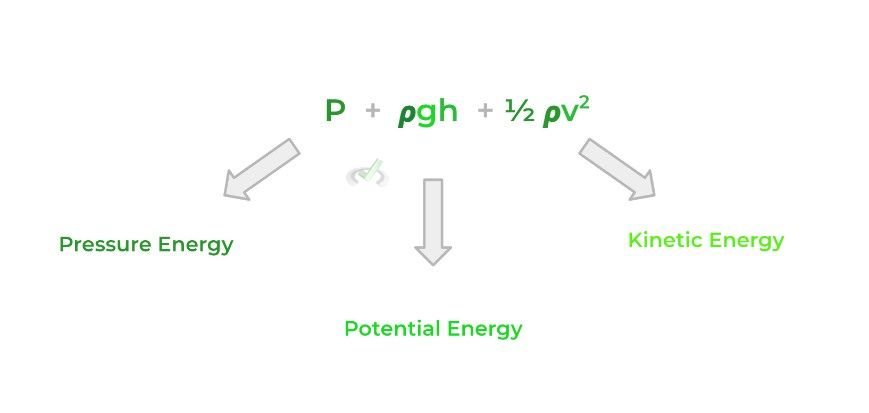
Finally, the final principle we’ll introduce is Bernoulli’s equation which is basically a reiteration of the law of energy conservation! As shown below, the equation can at first look very daunting and scary at first but can be broken down to where you simply have to realize that it’s an application of the conservation of energy!
Here, P simply refers to the pressure that a fluid places on a certain point which we can loosely call pressure energy. If you’ve noticed that the 𝞺gh value looked similar, that’s because it refers to the potential energy of the fluid at a certain height, just like gravitational potential energy!
Finally, the ½ 𝞺v2 may also look similar as it refers to the kinetic energy associated with fluid in motion! Let’s give a breakdown of each term and its associated energy!
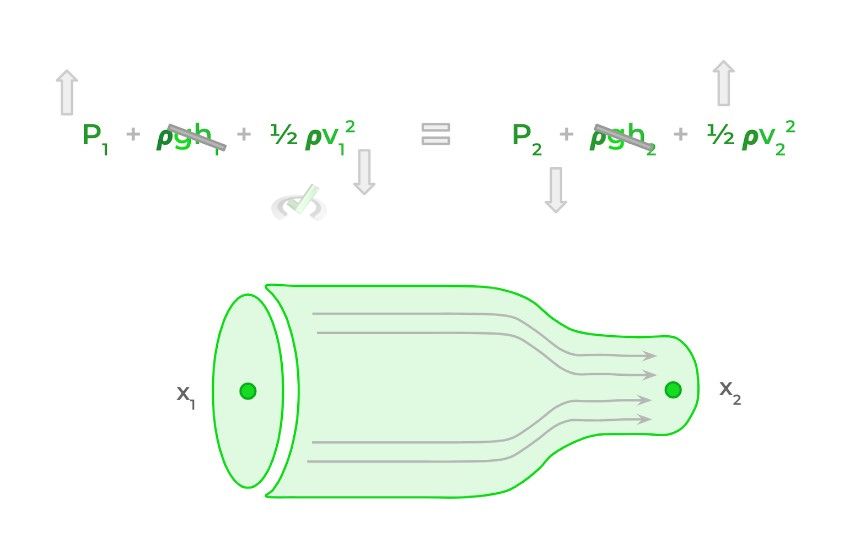
If we use a tube as a visual like the one shown above for the continuity equation, we can get a better idea of how to apply this equation. Because points 1 and 2 have the same height, they have the same potential energy which we can cross out.
Additionally, because point 2 has a smaller cross-sectional area, it has a faster velocity according to the continuity equation and thus has higher kinetic energy. Conversely, point 1 has a slower velocity and thus lower kinetic energy.
In order to have a conservation of energy, the only values that can balance out are the energy exerted by the pressure. Thus, the pressure at point 1 has to be greater than that of point 2 in order to maintain the conservation of energy. Think of the equation like a seesaw!
These equations should give a good introduction to the key fluid laws tested on the MCAT.
(Coming Soon!) Full Study Notes : Fluid Laws, Equations, and Effects
For more in-depth content review on fluid laws, equations, and effects, check out these detailed lesson notes created by top MCAT scorers.
3. Resistance
The final concept to keep in mind with fluids is resistance. Resistance in the system will decrease velocity. Greater resistance means it’s harder to flow. Resistance increases with decreased diameter and resistance decreases with increased diameter. It’s an inverse relationship.
This also can be directly applied to the circulatory system. Atherosclerosis is the buildup of cholesterol plaques in our arteries. This narrows the diameter of arteries and, therefore, increases resistance. This makes it harder for blood to flow, meaning the heart needs to work harder to keep up with the demands of our bodies.
(Coming Soon!) Full Study Notes : Resistance
For more in-depth content review on resistance, check out these detailed lesson notes created by top MCAT scorers.
4. Application of Fluid Dynamics in Physiology
The whole reason we study fluid dynamics in the first place, as much as we might not want to, is to use the basic fundamentals and apply them to our human physiology! The most obvious example of this is within the circulatory system!
Blood and lymph flowing within the circulatory system, more or less, follow the basic laws and equations of basic fluid dynamics. Of course, when dealing with the complexity of the circulatory system, alterations and exceptions must be made; however, the core elements remain the same!
Additionally, we can even apply elements of basic circuitry design to how blood vessels reduce resistance! Not only can we model the circulatory system as a closed circuit loop, we can also model how capillaries are arranged in parallel to reduce resistance!
We’ll discuss many of the broad applications of fluid dynamics (and even circuitry basics!) towards human physiology on the link below!
Pulmonary hypertension is characterised by intimal fibrosis of pulmonary arteries, atherosclerosis of the pulmonary trunk, hypoxic pulmonary vasoconstriction due to high altitude, or increased fluid volume in pulmonary circuit (left heart failure)
Resistance is inversely proportional to the 4th power of the radius of the blood vessel (Poiseuille’s)
(Coming Soon!) Full Study Notes : Application of Fluid Dynamics in Physiology
For more in-depth content review on application of fluid dynamics in physiology, check out these detailed lesson notes created by top MCAT scorers.
Important Definitions and Key Terms
Below are some high yield definitions and key terms to refer to when reviewing concepts and ideas about fluids!
Term | Definition |
|---|---|
Fluid | Describes a substance whose particles are free flowing allowing it to move freely and conform to any shape when placed into a container; Used to describe liquids and gasses |
Density | The ratio of an substance’s mass to its volume |
Specific Gravity | The ratio of an substance’s density to a reference density, usually water |
Cohesion | Intermolecular interactions between a fluid’s molecules which results in surface tension, allowing the surface of the fluid to resist tension when placed |
Adhesion | Favorable intermolecular interactions between a fluid’s molecules and a surrounding border which allows the fluid to “crawl” up the border |
Archimedes’ Principle |
States that when an object is submerged in a fluid, a buoyant force by the fluid is applied on the object in the upwards direction |
Buoyant Force |
Force generated by a fluid when an object is submerged |
Continuity Equation |
Gives an inversely proportional relationship between a fluid’s velocity and the tube’s cross-sectional area |
Bernoulli’s Equation |
Reiteration of law of energy conservation relating a fluid’s pressure, potential, and kinetic energy |
Additional FAQs - Fluids on the MCAT
Are Fluids on the MCAT?
Are Fluids Compressible? – MCAT?
What are the 3 Fluid Principles – MCAT?
What is a Fluid in Physics? – MCAT?
Additional Reading Links (Coming Soon!) – Study Notes for Fluids on the MCAT
Additional Reading: Physics Topics on the MCAT:
- Circuits on the MCAT
- Electrostatics on the MCAT
- Atomic and Nuclear Phenomena on the MCAT
- Kinematics on the MCAT
- Light and Optics on the MCAT
- Magnetism on the MCAT
- Thermodynamics on the MCAT
- Units and Dimensional Analysis on the MCAT
- Waves and Sound on the MCAT
- Work and Energy on the MCAT




 To help you achieve your goal MCAT score, we take turns hosting these
To help you achieve your goal MCAT score, we take turns hosting these