Confounding factors and statistical significance are key ideas in scientific research. They help us understand if study results are correct and what they mean. This guide will explain these ideas, their impact on research, and how they connect to other important topics.
I. Understanding Confounding Factors
Confounding factors are extra variables that can affect the outcome being studied (dependent variable) and the factor being tested (independent variable). Controlling them can lead to wrong conclusions about the relationship between these variables.
A. What Are Confounding Factors?
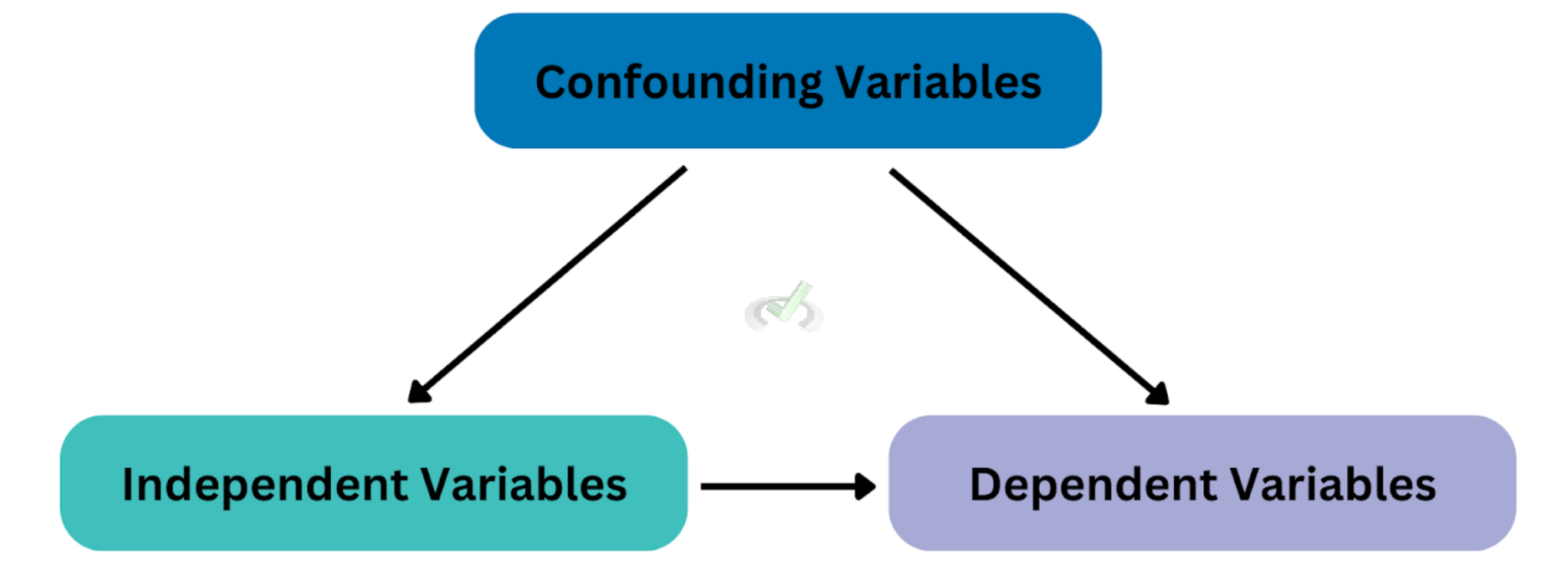
Confounding factors are extra variables that researchers didn't plan for. They can make it seem like a relationship between the variables being studied when there isn't one. For example, in a study on the effect of exercise on weight loss, diet could be a confounding factor. This is because diet also affects weight. If not controlled, it could make the results unclear.
B. Why Confounding Factors Matter
Controlling for confounding factors is crucial. They can distort the results of a study. This can exaggerate or hide the true effect of the independent variable. For example, a confounder might make a treatment seem effective when it is not. It could also hide the effectiveness of a useful treatment.
C. How to Control Confounding Factors
Researchers use several methods to control confounding factors:
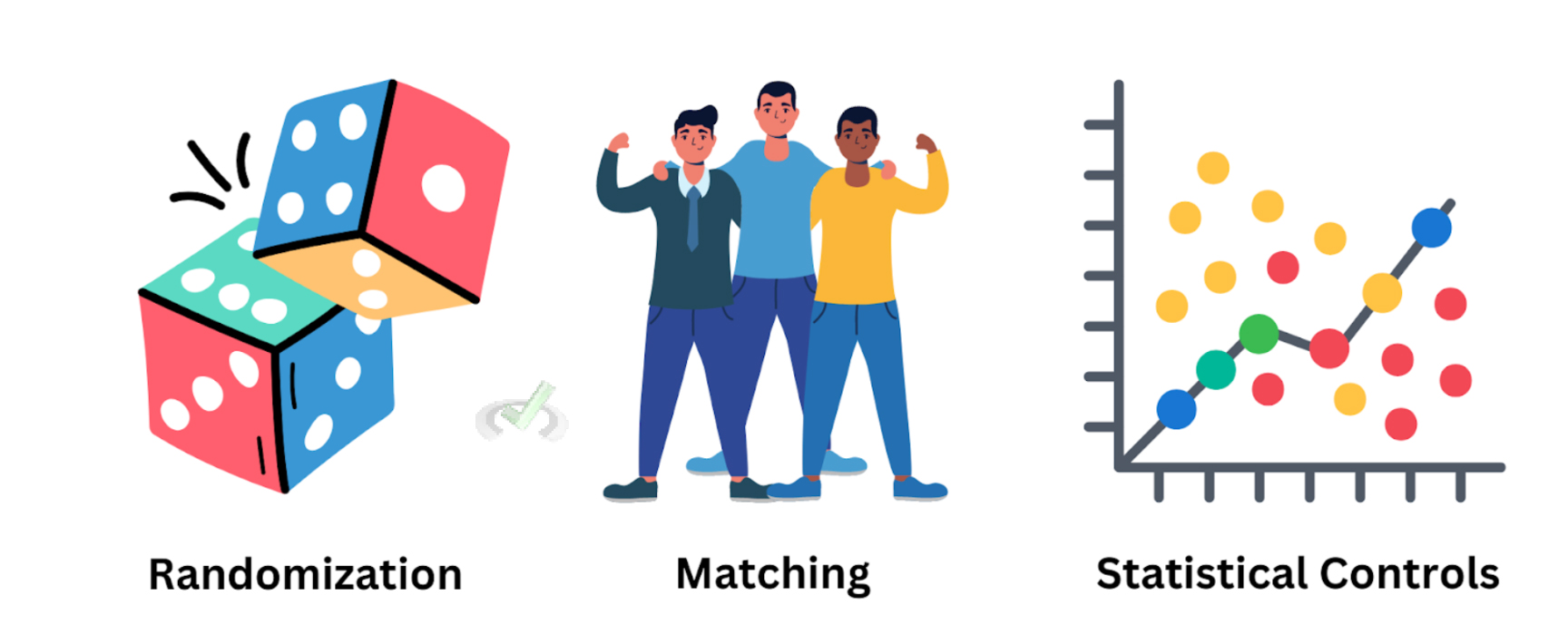
- Randomization: This involves randomly assigning participants to different groups. It helps ensure that confounding factors are evenly spread among the groups.
- Matching: This method ensures that groups have similar characteristics, like age or gender, which could affect the outcome.
- Statistical Controls: Researchers use methods like multivariate regression or analysis of covariance (ANCOVA). These methods adjust the data to reduce the effect of confounders.
II. Statistical Significance: What Does It Mean?
Statistical significance helps researchers decide whether a study's results are likely due to the effect being tested or just by chance.

A. Defining Statistical Significance
Statistical significance is often shown by a p-value. The p-value tells us the chance that the results happened by accident. A p-value of less than 0.05 is commonly used to show statistical significance. This means there's less than a 5% chance that the results happened accidentally.
B. Importance of Statistical Significance
Statistical significance shows whether the findings of a study are reliable. However, it doesn't always mean the findings are important or useful. For example, a treatment might have a statistically significant effect. However, if the effect size is very small, it might not be meaningful in real life.
C. Misinterpretations of Statistical Significance
Thinking that statistical significance alone makes a result important or true is a mistake. A result can be statistically significant but not practically significant. This means it has little real-world impact. For example, a drug might lower blood pressure by a statistically significant amount. But if the actual change is tiny, it might not be clinically relevant.
III. The Relationship Between Confounding Factors and Statistical Significance
Confounding factors can affect the statistical significance of study results. If these factors are not controlled, they can lead to false findings. This might hide a real effect or create the illusion of an effect where there is none. It's essential to account for confounding factors to ensure that statistically significant results reflect a true effect.
IV. Bridge/Overlap
Understanding confounding factors and statistical significance is essential not only in research but also in real-world applications.
A. Research Integrity and Validity
Properly addressing confounding factors and interpreting statistical significance are crucial for keeping research trustworthy. They ensure that study conclusions are based on correct and reliable data.
B. Decision-Making in Public Policy and Medicine
Decisions often rely on research findings in fields like public policy and medicine. Ensuring these findings are statistically significant and free from confounding factors helps make better decisions based on evidence. For instance, in medicine, deciding whether to approve a new drug depends heavily on understanding these ideas.
C. Epidemiology and Public Health
In epidemiology, understanding confounding factors is crucial for identifying disease risk factors. For example, a study might find that people who smoke are more likely to have lung cancer. However, if not controlled, a confounding factor like asbestos exposure (which also causes lung cancer) could distort these results.
D. Psychological and Behavioral Sciences
In psychological research, statistical significance and confounding factors are key in studying human behavior and mental processes. For example, researchers must account for confounding factors like socioeconomic status when studying the impact of education on brain development.
V. Wrap Up/Key Terms
Understanding confounding factors and statistical significance is crucial for correctly interpreting scientific studies. Controlling for confounding factors ensures valid study results. Understanding statistical significance helps assess the reliability of these findings.
Key Terms
- Confounding Factors: Extra variables that can affect both the dependent and independent variables. They can distort study results.
- Randomization: Assigning participants to different groups randomly to control for confounding factors.
- P-value: A statistical measure showing the chance that study results happened accidentally.
- Statistical Significance is the likelihood that study results are due to a specific factor rather than chance. It is often shown by a p-value of less than 0.05.
- Effect Size: A measure of the strength or size of a treatment effect or association.
VI. Practice Questions
Sample Practice Question 1
In a study examining the relationship between coffee consumption and alertness, which of the following could be a confounding factor?
A. Amount of sleep
B. Gender
C. Age
D. All of the above
Ans. D
All these factors (amount of sleep, gender, and age) can affect alertness independently of coffee consumption. If not controlled, they could distort the relationship between coffee consumption and alertness.
Sample Practice Question 2
If a study finds a p-value of 0.03, what does this indicate about the statistical significance of the results?
A. The results are likely due to chance
B. The results are statistically significant
C. The results are not statistically significant
D. The study was flawed
Ans. B
A p-value of 0.03 indicates a 3% chance that the results occurred by random chance. This is below the common threshold of 0.05. Therefore, the results are considered statistically significant. This suggests a real effect rather than a random occurrence.





 To help you achieve your goal MCAT score, we take turns hosting these
To help you achieve your goal MCAT score, we take turns hosting these 






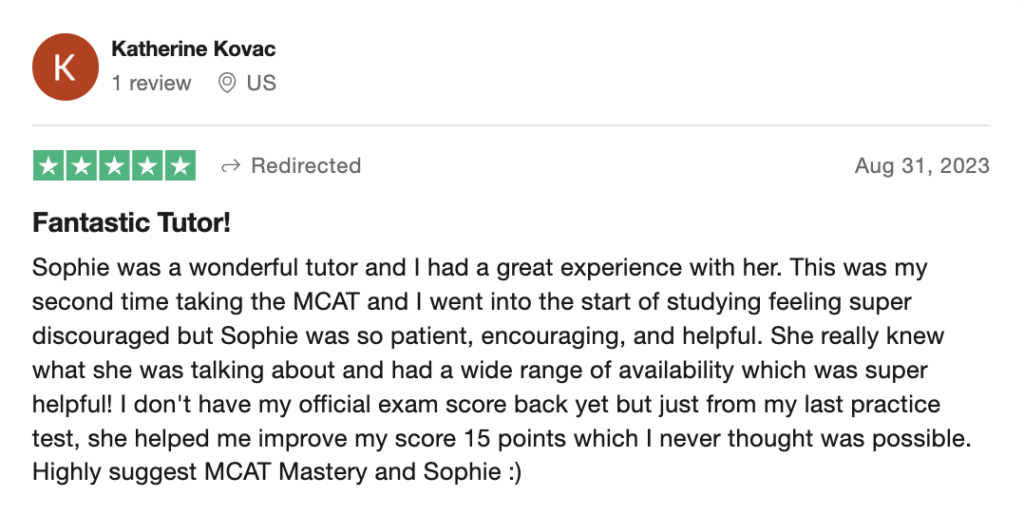


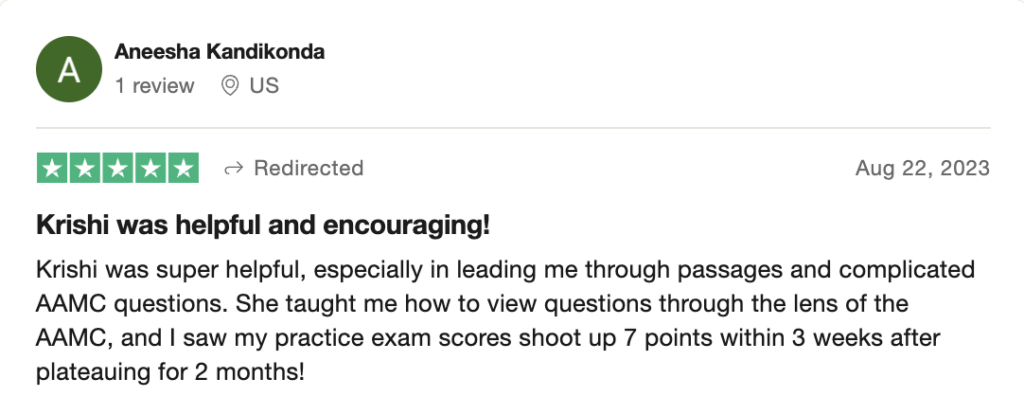
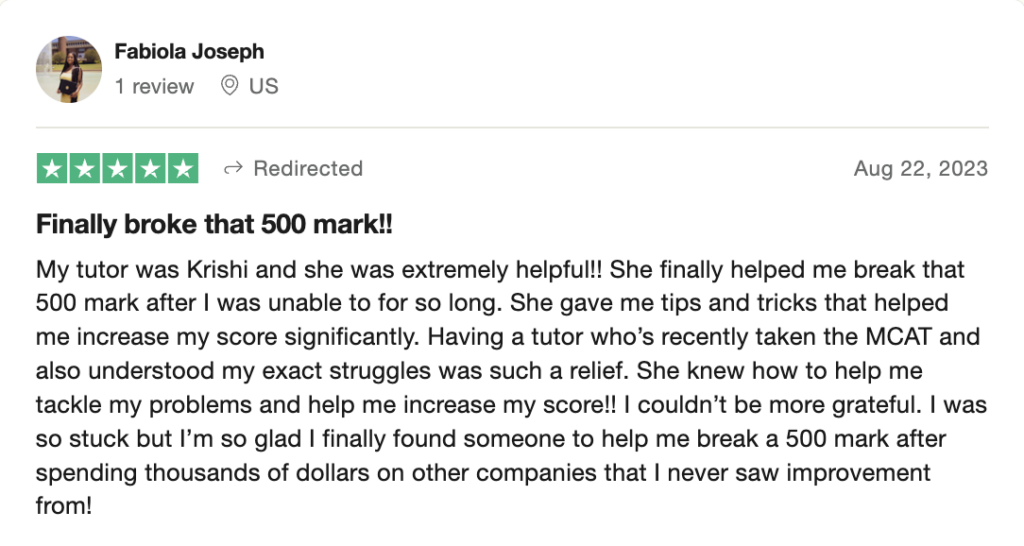
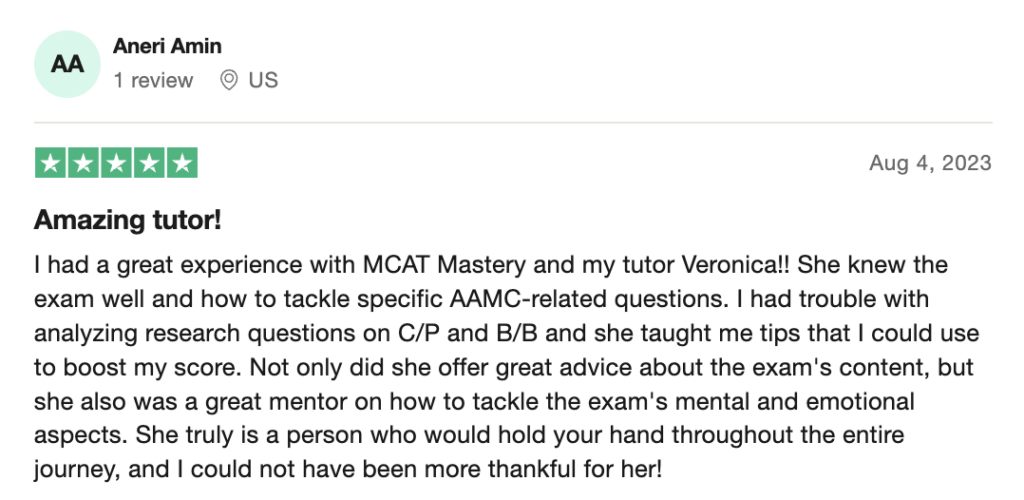


 reviews on TrustPilot
reviews on TrustPilot