In the MCAT, you will probably encounter problems with growth or decay. Unfortunately, you have to learn the basics of these concepts before going into the formulas themselves. Exponents and logarithms are mathematical concepts used to define the change in a certain quantity as a function. These are useful tools. However, there are laws to remember before going right in and solving these problems. In this article, we’re looking at the laws of logarithms and exponents so you can be more confident when you see them in the MCAT.
I. Laws of Exponents
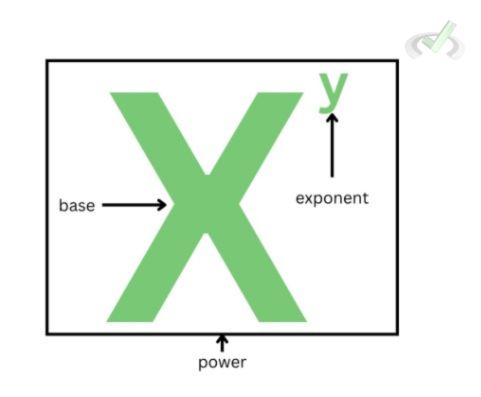
Exponents are mathematical notations that indicate the number of times a number is multiplied by itself. In the expression 5³, we see two numbers. Five is our base, and the superscript three is our exponent. The whole expression is known as a power. The expression 5³ means that we multiply the number 5 by itself 3 times.
5³ = 5 x 5 x 5
One important skill when solving problems in math is mastering the laws of exponents. The laws of exponents are rules to follow when handling exponents. Unlike normal numbers, where we can directly do operations without much thought, exponents must be handled carefully. Otherwise, a math problem will always fail.
Product of powers
When multiplying numbers with exponents or powers, a product of powers says that when we multiply powers with the same base, we can copy the base and add the exponents.

Let’s try this:
10³ x 10⁴
Since we have the same base, according to the product of powers, we can copy the same base and directly add the exponents as the final answer.
10³ x 10⁴ = 10³⁺⁴
10³ x 10⁴ = 10⁷
We cannot follow the same rule if we’re handling powers with different bases. The law requires two powers to have equal bases.
Quotient of Powers
In this law, the same rule applies to having equal bases. When dividing powers with the same bases, we can copy the common base and subtract the exponent at the denominator from the exponent at the numerator to get the answer.
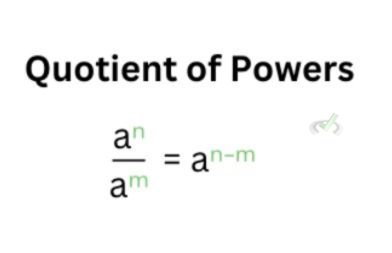
Let’s look at one example:
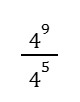
To get the difference, we copy 4 and subtract the exponent at the denominator (5) from the exponent at the numerator (9).
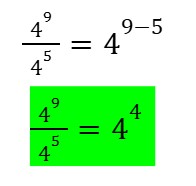
Power of Powers
When a power is raised to another number, we use the same base and multiply the exponents.

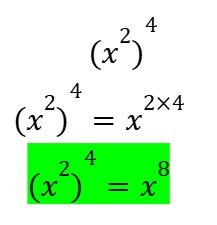
Negative Powers
This rule states that when a base has a negative exponent, it’s also equal to the reciprocal of the base raised to the now positive exponent.
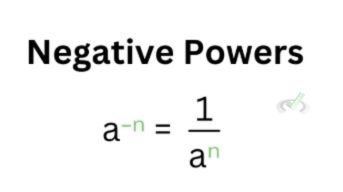
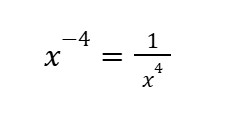
Zero Exponent
The rule of zero exponents merely states that any nonzero number raised to zero is equal to one.

x ⁰ = 1
II. Laws of Logarithms
Logarithms are simply the inverse of exponents. Let’s look at the parts of exponents.
We have x raised to y, which has a value of z.
Using the logarithm, we can rewrite this as the log of z base x is equal to y. We use logarithms to write exponents as a function. This way, we can relate the exponentiation of a value as a function. As the inverse of exponents, logarithms solve for the exponent when we have the base and the value available.
A function shows changes in a dependent variable in relation to the independent variable. In the same way, logarithms show how many times a base must be multiplied by itself to get a desired value. We use logarithms to predict the growth or decay of population, bacteria, money, or other desired subjects.
Three important laws of logarithms exist: the product rule, the quotient rule, and the power rule.
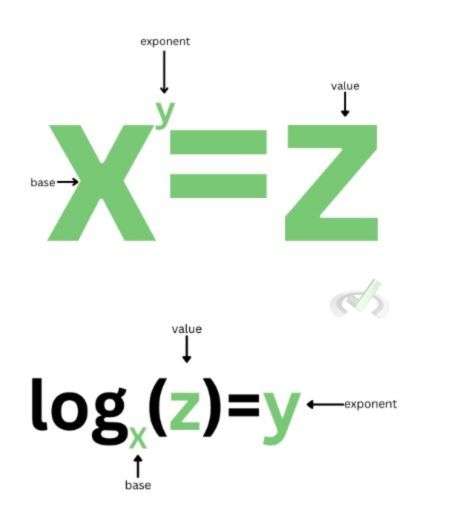
Product Rule
These laws of logarithms assume the same base. In the product rule, the logarithm of a product (xy) is also equal to the sum of the logarithm of its factors (x and y).
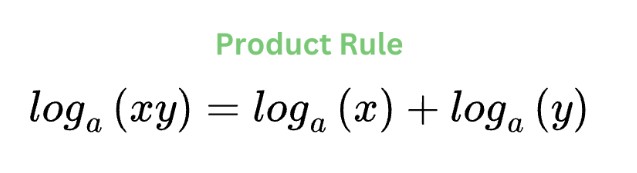
Example:
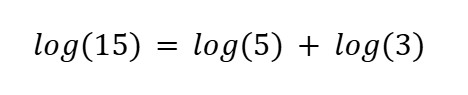
Quotient Rule
The logarithm of a quotient is equal to the difference between the logarithm of the numerator or dividend and the denominator or divisor.
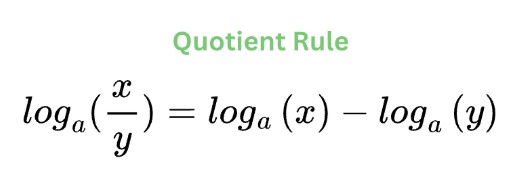
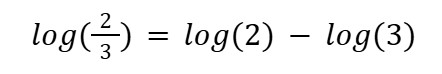
Power Rule
The logarithm of a number (x) raised to an exponent (n) is equal to the exponent (n) multiplied by the logarithm of the same number (x)

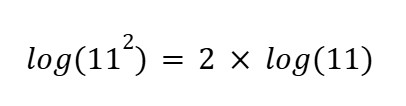
III. Natural Logarithm
A natural logarithm is a logarithm with a mathematical constant as a base known as Euler’s constant or simply e (approximately equal to 2.718). This constant was derived as the limit of an expression as it reaches infinity. Natural logarithms follow the same rules as logarithms. As we previously discussed, you only need to know a few facts about the natural logarithm.

IV. Summary
Logarithms and exponents are crucial concepts not just in mathematics but also in science. We use these concepts to look at changes in a particular quantity over time. We use the same concept to predict the growth of cells, the decay of isotopes, or the progression of diseases. Mastering the laws of exponents and logarithms is an essential skill that you will find useful in other articles as you go through other subjects.






 To help you achieve your goal MCAT score, we take turns hosting these
To help you achieve your goal MCAT score, we take turns hosting these 









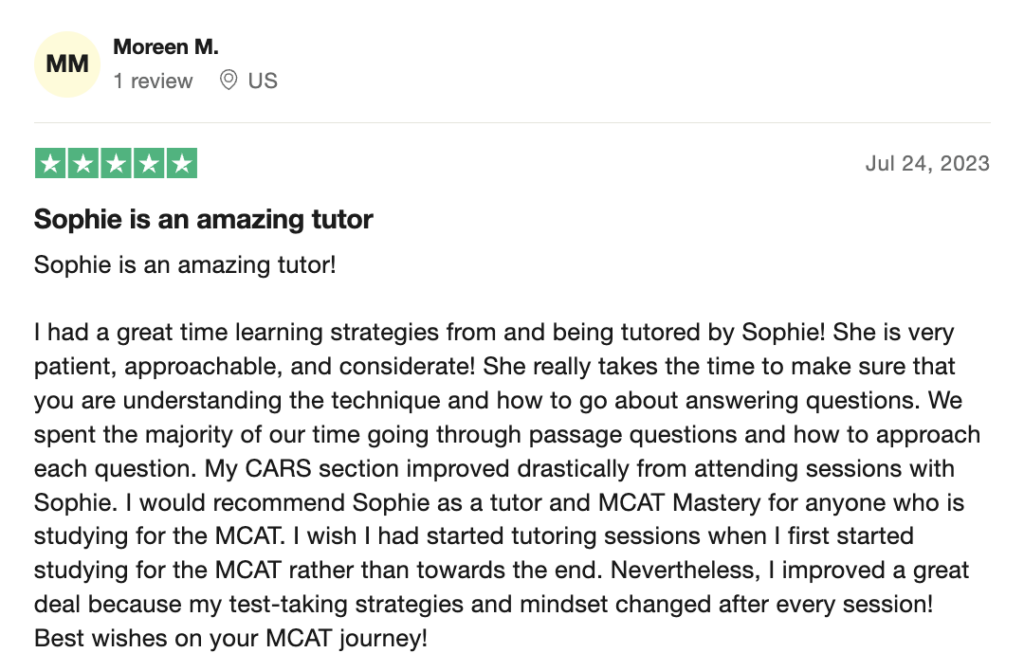

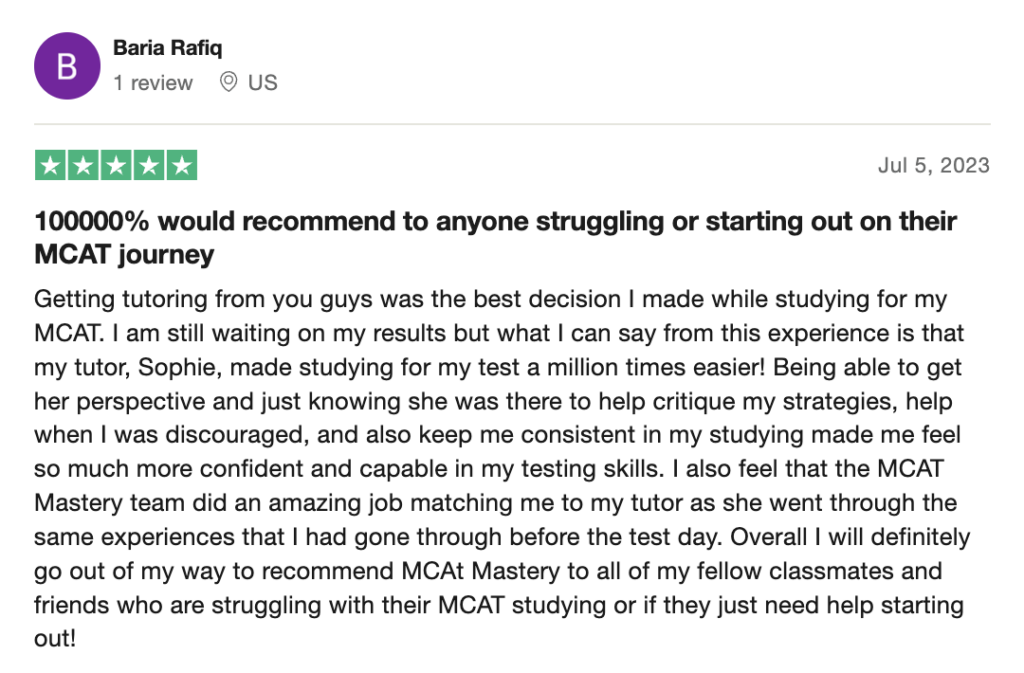
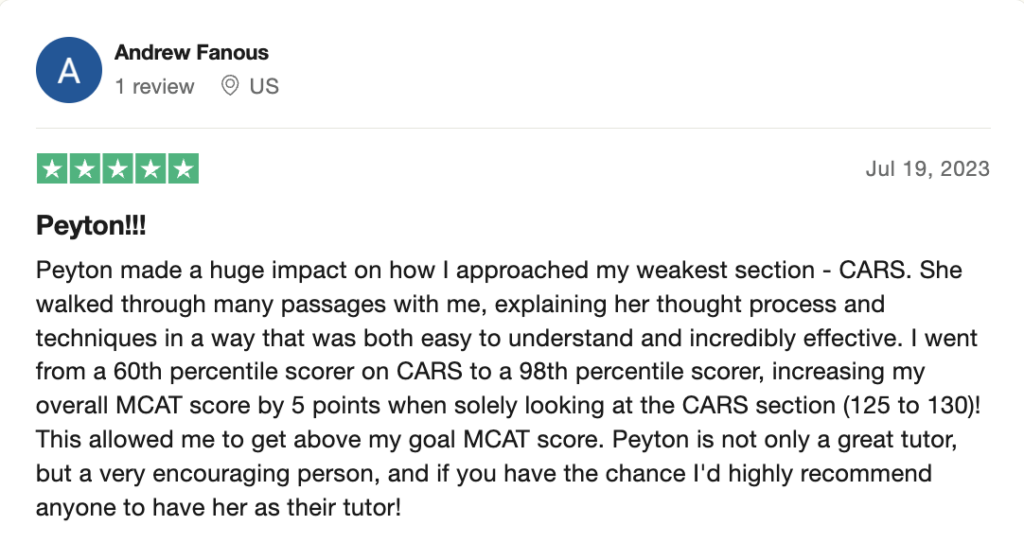
 reviews on TrustPilot
reviews on TrustPilot