Understanding Coulomb's Law is fundamental in physics. It describes how charged particles interact, crucial for comprehending electricity and magnetism. Let's examine the principles of Coulomb's Law and see how they shape our understanding of electric forces.
I. Introduction to Coulomb's Law
When you rub a balloon on your hair and then stick it to a wall, it clings because of electric charges. Coulomb's Law explains the strength of this electric force between two charged objects.
Coulomb's Law explains that the electric force between two charged objects depends on their charges and distance. The formula is:
Where:
- F is the force between the charges
- k is Coulomb's constant:
- q1 and q2 are the magnitudes of the charges
- r is the distance between the charges
II. Key Concepts in Coulomb's Law
Let's explore the key concepts that make up Coulomb's Law. Understanding these principles will help you grasp how electric forces work and apply this knowledge to various scenarios.
Electric Charges
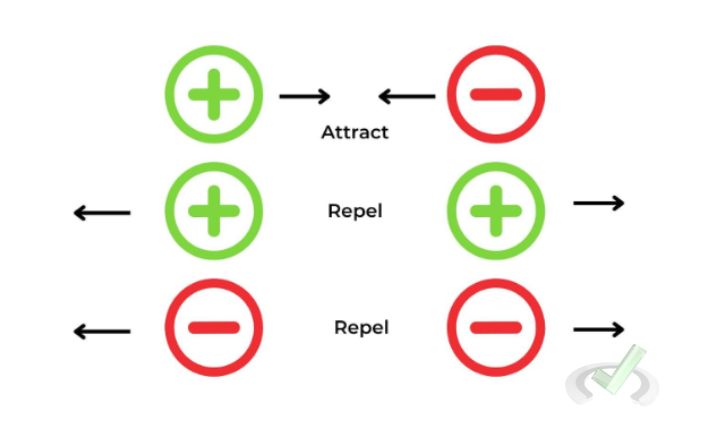
Charges come in two types, positive and negative, where like charges repel one another and opposite charges attract. This attraction or repulsion is the basis of Coulomb's Law.
The unit of charge is called Coulomb (C). Electrons carry a negative charge, and protons have a positive charge.
Example: If you have two positive charges, they will push away from each other. They will pull towards each other if you have one positive and one negative charge.
Coulomb's Constant
Coulomb's constant k is a number that makes the equation work with the units we use for charge and distance. Its value is:
This constant helps us calculate the force between charges accurately.
Example: When calculating the force between two charges, the constant ensures the units for force (Newtons) are correct, making our calculations meaningful.
Distance and Force
The distance r between the charges significantly affects the force. If the distance doubles, the force reduces to a quarter of its original value because the force is inversely proportional to the square of the distance.
Example: If two charges are 1 meter apart and exert a force of 10 N on each other, moving them to 2 meters apart will reduce the force to 2.5 N.
Magnitude of Charges
The product of the magnitudes of the charges (q1×q2q1×q2) determines how strong the force will be. Larger charges produce a stronger force.
Example: Doubling the charge on one of the objects will double the force between them. If both charges are doubled, the force will be four times as strong.III. Applications of Coulomb's Law
Coulomb's Law has many practical applications. It helps us understand electric fields and is crucial in everyday situations and technologies.
Electric Fields
Coulomb's Law helps us understand electric fields. An electric field is the area around a charged object where other charges feel a force. The strength of this field can be calculated using Coulomb's Law and is given by the formula:
Where:
- E is the electric field strength
- q is the charge creating the field
- r is the distance from the charge
Example: If you place a small positive test charge near a larger positive charge, the test charge will experience a force pushing it away, showing the presence of an electric field.
Everyday Examples
- Static Electricity: Imagine the time when you rub a balloon on your hair, electrons transfer between the two, causing a static charge. Then when you put the balloon to the wall, it sticks because opposite charges attract.
- Electronics: The behavior of components in circuits, like capacitors and resistors, depends on the principles of Coulomb's Law. Capacitors store energy in the electric field created between two opposite charges on conductive plates.
IV. Bridging Coulomb's Law with Other Concepts
Coulomb's Law Is connected to many other important concepts in physics. Understanding these connections can help you see the broader implications of electric forces.
Electric Potential Energy
Just as gravity gives potential energy to objects with mass, charges have electric potential energy. This energy depends on the position of the charges and can be calculated using Coulomb's Law.
Where U is the electric potential energy.
Example: If you have two charges close together, separating them requires work because they attract each other. This work becomes stored as electric potential energy.
Electric Potential
Electric potential (V) is the potential energy per unit charge. It can be calculated by:
Where electric potential is measured in volts (V).
Example: The electric potential near a charged object shows how much potential energy a test charge would have at that location.
Molecular Forces
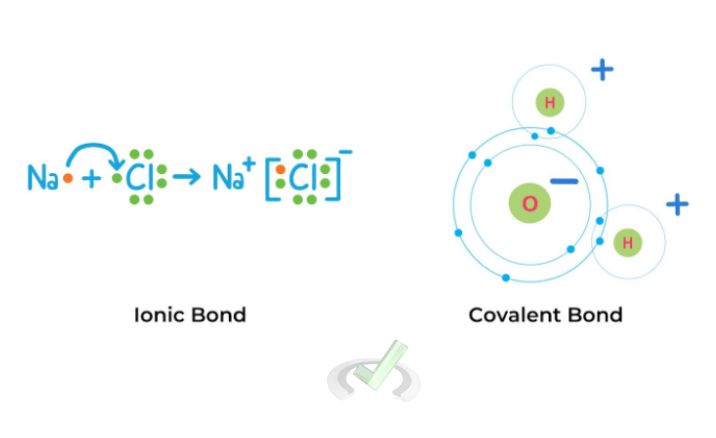
Coulomb's Law explains the forces between charged particles in atoms and molecules at a molecular level. This is important in chemistry and biology for understanding bonds and interactions, such as ionic and covalent bonds.
Example: In an ionic bond, positively and negatively charged ions attract each other, forming a stable compound like sodium chloride (table salt).
Magnetism
Though Coulomb's Law deals with electric forces, it also relates to magnetism. Moving electric charges create magnetic fields, linking the two phenomena. This relationship is explained by the Biot-Savart Law and Ampère's Law.
Example: Electric currents in wires create magnetic fields around them, which is the principle behind electromagnets.VI. Wrap-Up and Key Terms
Coulomb's Law is a cornerstone of electrostatics. It explains how electric charges interact and quantitatively describes the forces between charged objects.
This law is foundational in physics and bridges to other crucial topics like electric fields, potential energy, molecular forces, and magnetism. Understanding these concepts is essential for delving deeper into more advanced topics in physics and related fields.
Key Points:
Electric Charges: Positive and negative charges that exert forces on each other.
Coulomb's Law: Formula that calculates the electric force between two charges.
Coulomb's Constant: Proportionality factor in Coulomb's Law.
Electric Fields: Areas around charged objects where other charges experience force.
Electric Potential Energy: Energy due to the position of charges.
Electric Potential: Potential energy per unit charge.
Molecular Forces: Forces between charged particles in atoms and molecules.
Magnetism: Relationship between electric charges and magnetic fields.
V. Practice Questions
Sample Practice Question 1
What happens to the force between two charges if their distance is tripled?
A. It stays the same.
B. It triples.
C. It becomes one-third.
D. It becomes one-ninth.
Ans. D
According to Coulomb's Law, the force is inversely proportional to the square of the distance. Tripling the distance reduces the force to 132=19.
Sample Practice Question 2
What happens to the force between them if one charge is doubled and the other is tripled?
A. It stays the same.
B. It doubles.
C. It triples.
D. It becomes six times greater.
Ans. D
The force is directly proportional to the product of the charges. Doubling one charge and tripling the other increases the force by 2×3=6.


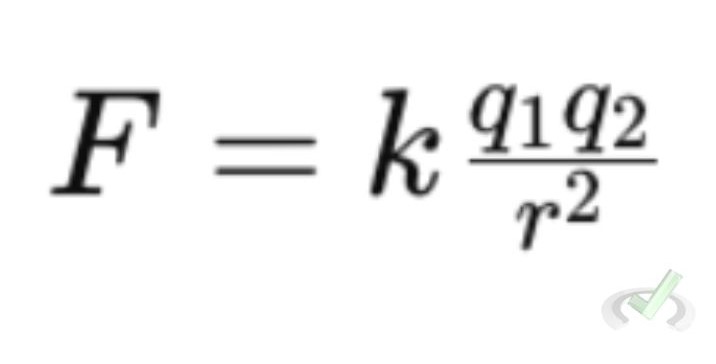
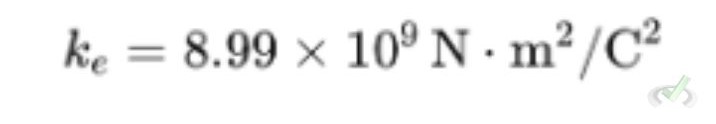
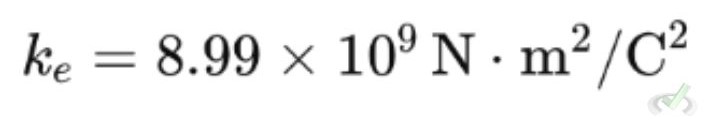

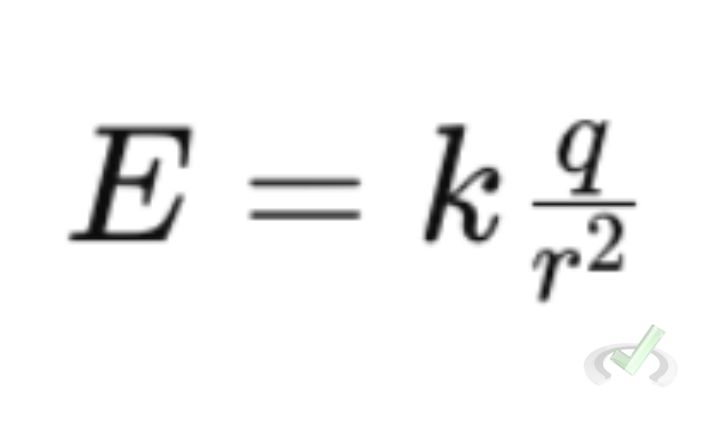
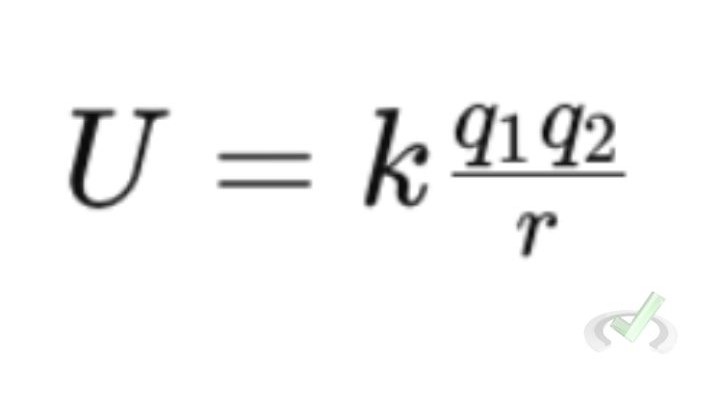
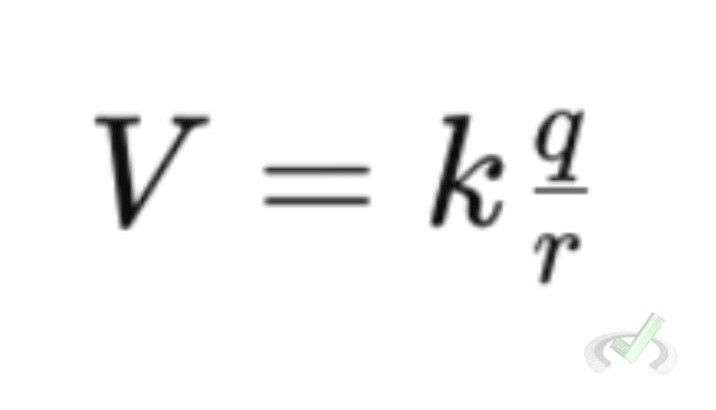



 To help you achieve your goal MCAT score, we take turns hosting these
To help you achieve your goal MCAT score, we take turns hosting these 








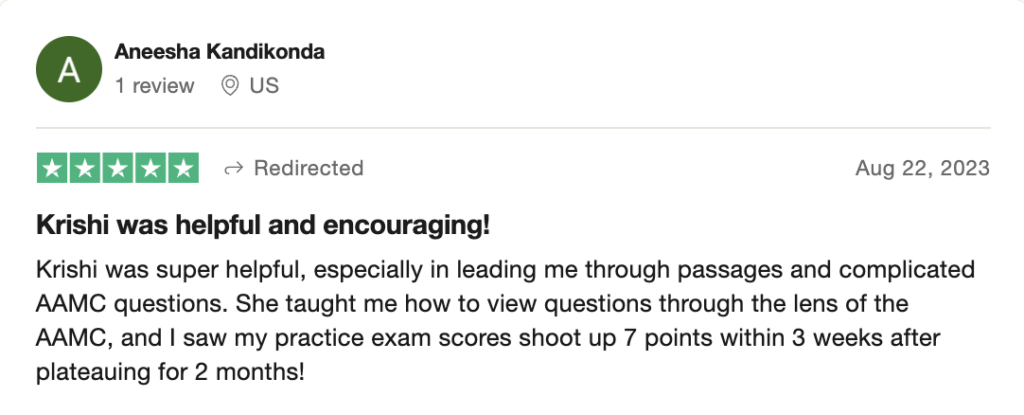
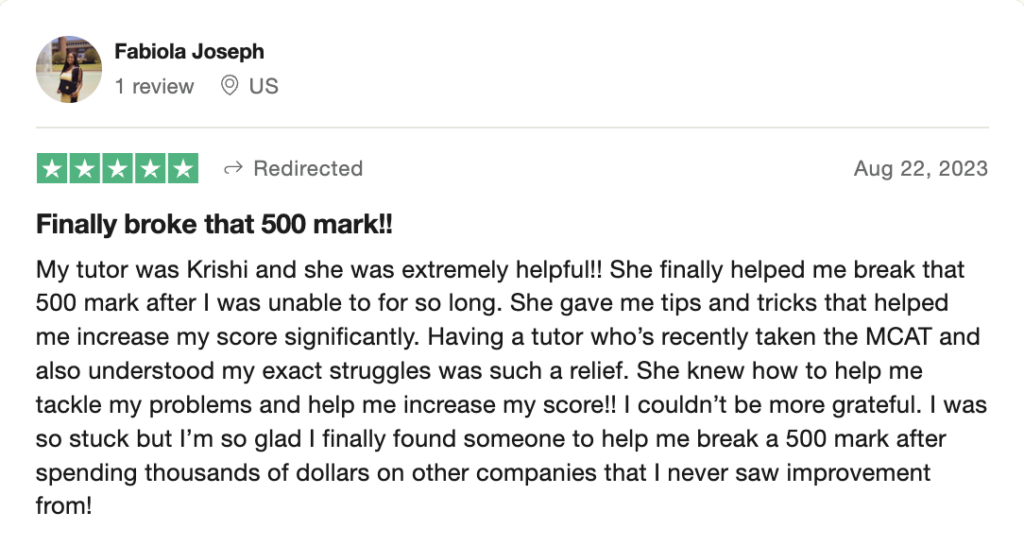
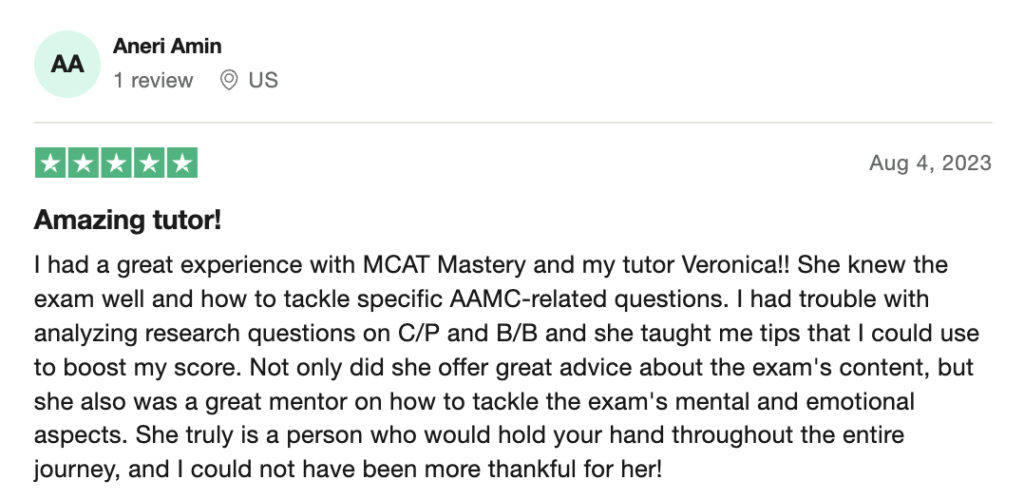

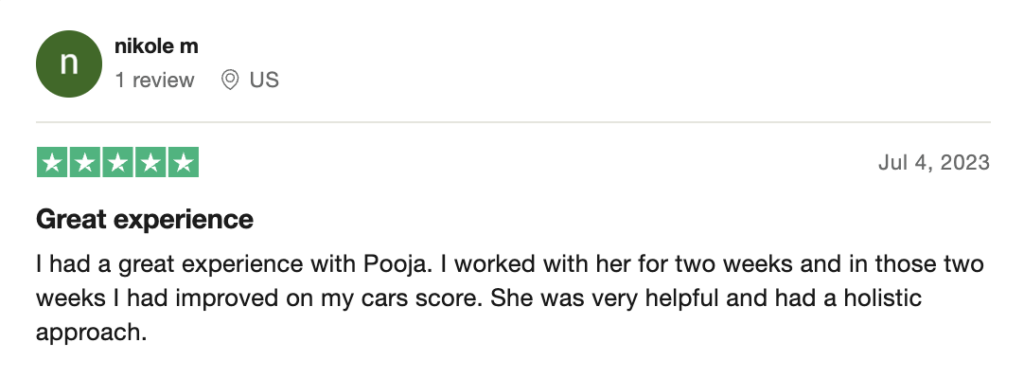
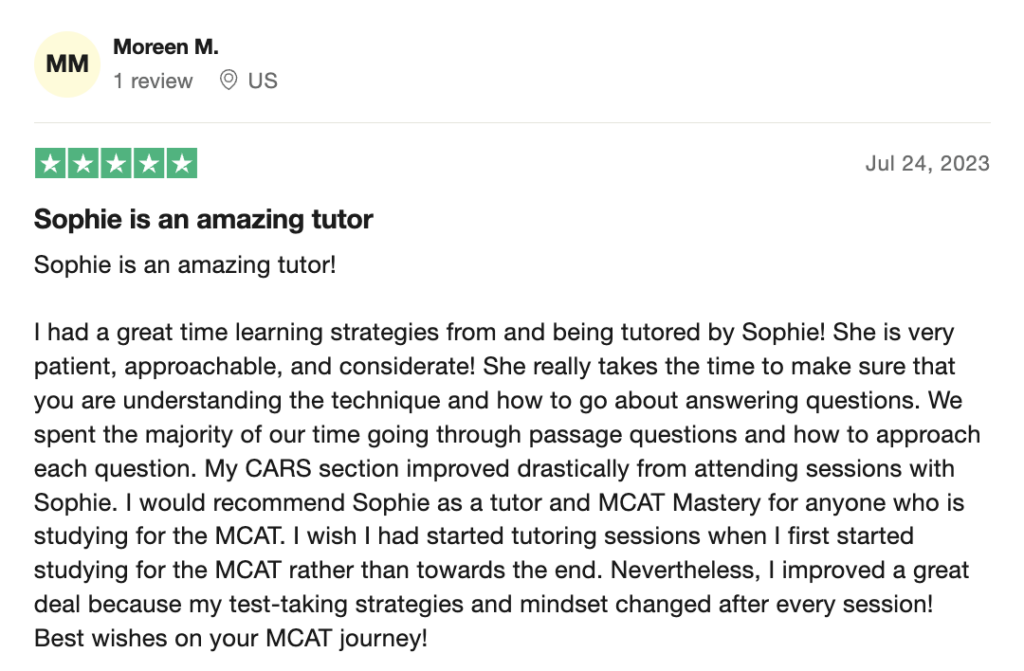

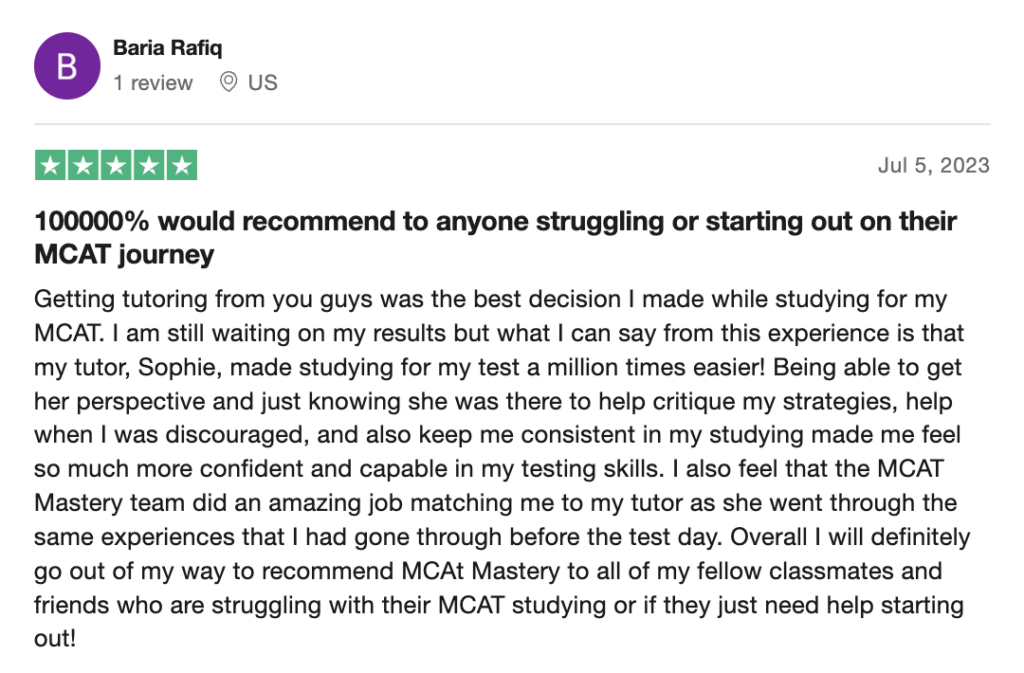
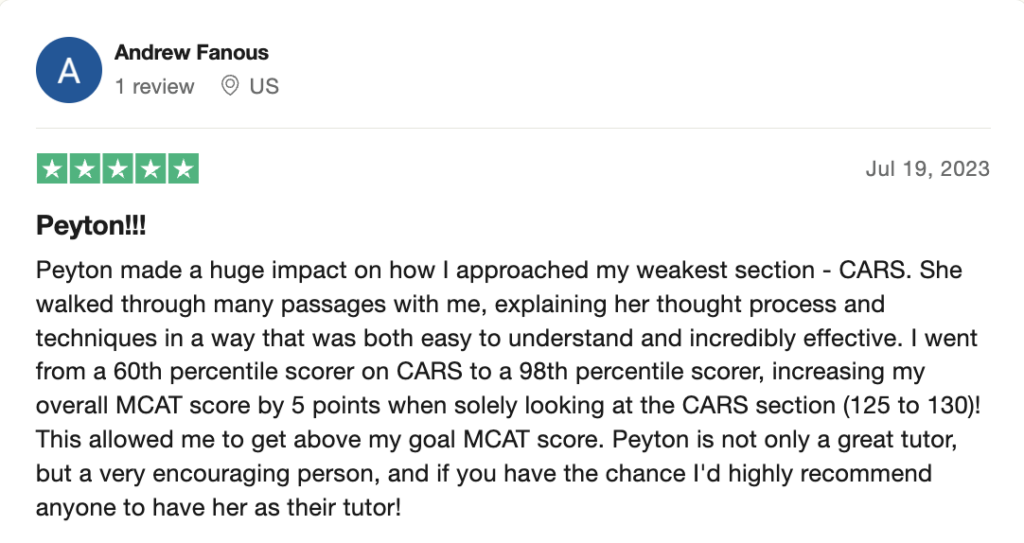
 reviews on TrustPilot
reviews on TrustPilot