Now that weโve discussed the basics of chemical kinetics and the theories that affect it, letโs examine how these concepts apply.
From our previous articles, weโve sorted out that in chemical kinetics, weโre concerned with the rate of reaction or how fast a reaction takes place. We specifically defined reaction rate as how fast a reactant disappears or how fast a product appears.
I. Reaction Rate
To begin, letโs understand the concept of reaction rates. The reaction rate tells us how fast a reaction occurs. As such, we calculate the reaction rate based on the rate of disappearance of reactants and the rate of appearance of products.
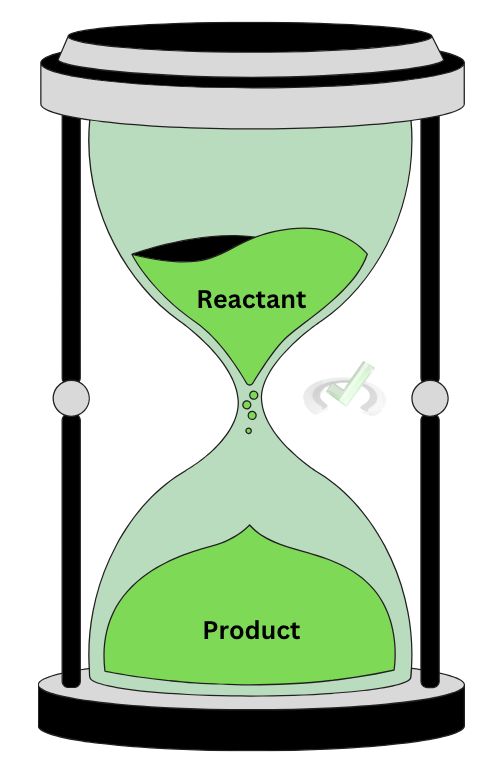
Think of it using an hourglass. When reactants disappear, more products form. When reactants are consumed, they are transformed into a new product. This makes sense since the rate of reaction is concerned with how fast a reaction occurs. A reaction occurs once reactants are transformed into products!
Letโs take a look at what that means using the equation below.
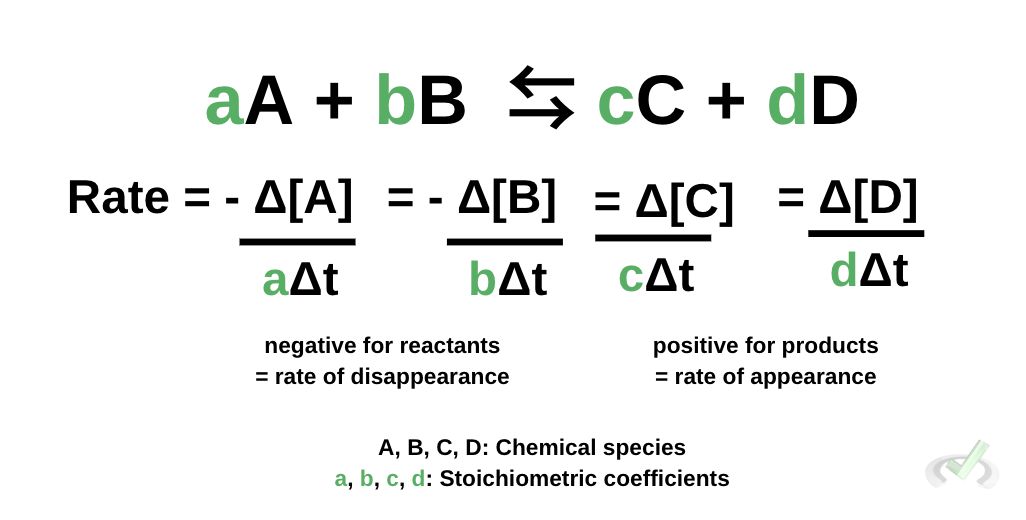
Here, we use a theoretical reaction between the reactants A and B to form products C and D. We also use lowercase letters to represent their stoichiometric or numerical coefficients when written.
We calculate the rate of reaction using the concentration of the reactants and the products. For reactants, we use the negative concentration of the reactants divided by the time elapsed multiplied by their respective coefficient. We use a negative sign for reactants since weโre concerned with the rate of disappearance. Accounting for the disappearance is represented by the negative sign.
We determine the rate of reaction for products using the same formula, the only difference being the positive sign used for products. Because weโre concerned with the rate of appearance, the sign becomes positive.
Note that brackets represent the concentration of a chemical species. When we see [X], it simply means weโre pertaining to the concentration of X.
II. Rate Law
Another way to determine the rate of reaction is to use the rate law equation. The rate law equation uses a rate constant k to determine the rate of reaction.
The constant k is a rate constant determined experimentally. Its value is usually already given. This constant depends on the nature of the reactants, temperature, and others. While it may seem like an outlandish value, it is simply a rate constant specific to the reaction. Its value is usually given in problems.
Before we begin to try out the rate law for ourselves, itโs best to understand the rate law using examples. IIn the first example, the rate of reaction in an unimolecular reaction is simply the rate constant k multiplied by the concentration of the reactant, A raised to the order of reaction, 1. The order of reaction is simply the stoichiometric coefficient of the reactant. In this case, we no longer need to put 1 beside A since itโs already understood that there is 1 mole of A in the reaction.
For a bimolecular reaction involving reactants A and B, the rate of reaction is equal to the rate constant k multiplied by the product of the concentration of A raised to 1, and the concentration of B raised to 2. We raise the concentration of B to 2 since we have 2 as the stoichiometric coefficient, 2, beside B.
In a termolecular reaction such as the reaction shown below, the rate of reaction is equal to the rate constant, k, multiplied to the product of the concentration of A raised to 2, B raised to 3, and C raised to 1.
The exponents that are put on the concentration of reactants are the order of reaction with respect to the reactant.
III. Reaction Rates Using Experimental Data
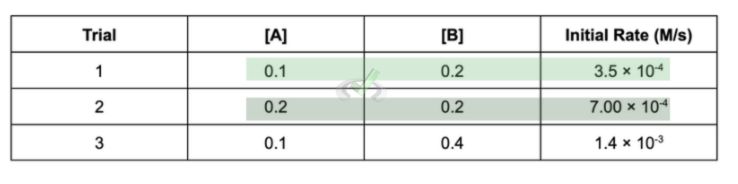
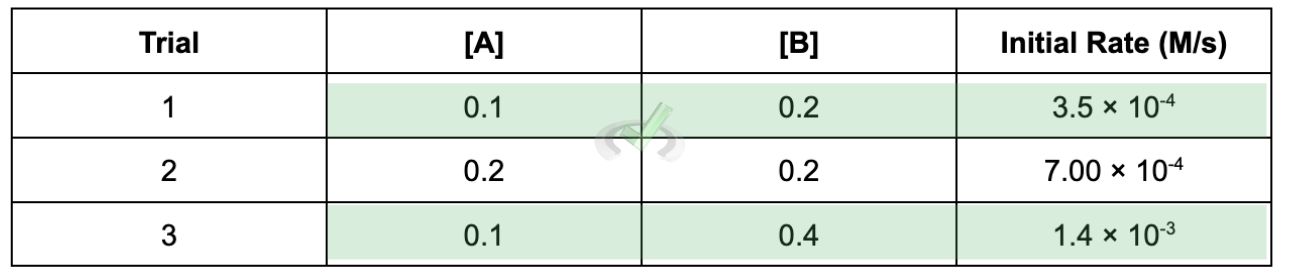
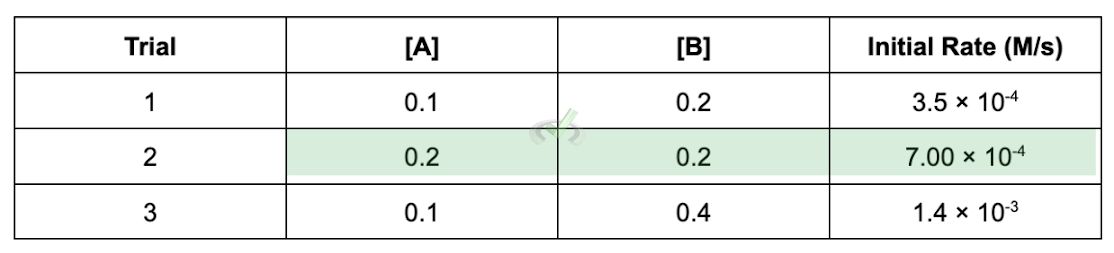
Sometimes, experimental data in a reaction is already given. Say we have a reaction between the reactants A and B to make C. What data will usually tell us is the concentration of the reactants on various trials and the initial rates of reaction for that trial.
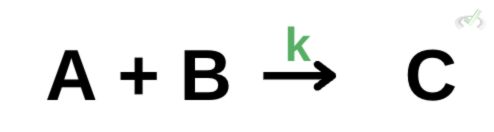
The data should look like this:
Trial | [A] | [B] | [Initial Rate (M/s)] |
|---|---|---|---|
1 | 0.1 | 0.2 | 3.5 ร 10โปโด |
2 | 0.2 | 0.2 | 7 ร 10โปโด |
3 | 0.1 | 0.4 | 1.4 ร 10โปยณ |
In problems like these, youโll usually be asked to figure out the rate constant k. This value is important as it is a constant specific for a reaction. The first thing you need to remember is that we get the value for the rate constant by comparing the various trials of experiments done.
For any reaction, the rate law states that the rate of reaction is equal to the constant k multiplied to the concentration of the reactants raised to their respective order. With problems like these, we need to determine what these orders are before we figure out the value for the rate constant k.
Step 1: Determine the Order of Reaction
Previously, we took these orders as the numerical coefficient of the reactants. However, this can also be found from experimental data. Notice how in various trials, there were changes in the concentrations of the reactants and the initial rates of reaction.
We get the order of reaction for each reactant first. We do this by comparing the data from the trials. For this reaction, letโs compare trials 1 and 2. Note that it doesnโt matter which trials youโll compare first, the order of reaction will always remain the same!
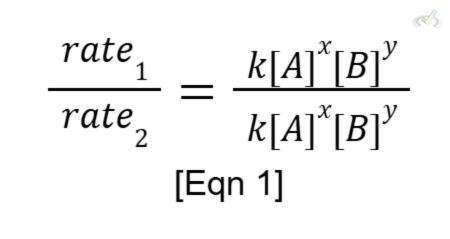
Setting up the equation using equation 1,
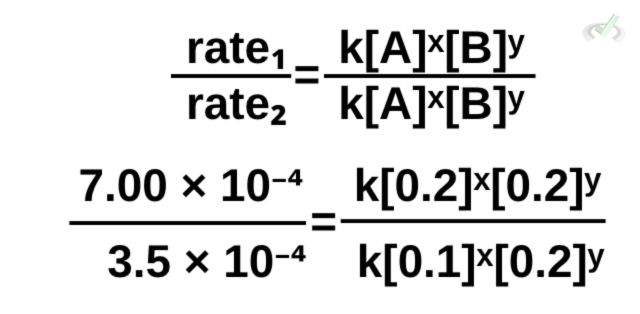
Notice how we have like terms on both the numerator and the denominator. We can proceed to cancel k and [0.2]สธ.
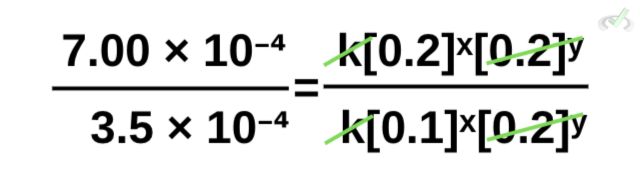
Rewriting this and removing the canceled terms,
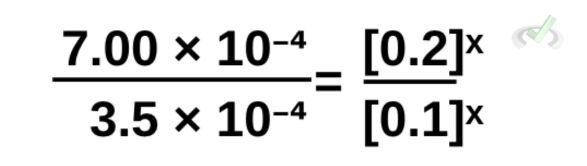
We can simplify this further by dividing the left side of the equation. From the rules of exponents, the right side of the equation is also equal to [(0.2)/(0.1)]หฃ.
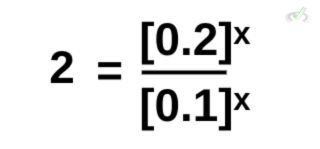
Calculating further, we get:
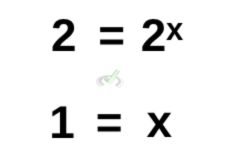
Remember that from the laws of exponents, if numbers have the same base, in this case both sides have a base of 2, their exponents equate to each other. A number with no exponent is also automatically equal to 1.
As such, the order of reaction with respect to A is equal to 1.
Now, letโs figure out the rate of reaction with respect to B.
This time, letโs use the same equation, but letโs use data from trials 1 and 3.
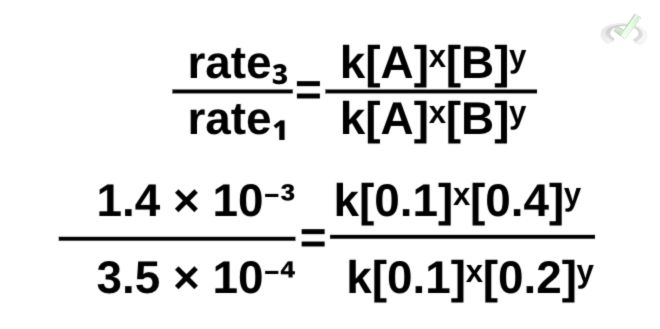
Note that you can choose to put any trial on top of another (rate 1/rate 3), and the result will still be the same. Itโs simply easier for us to view things mathematically if we put the larger value on top.
Now, letโs cancel terms.
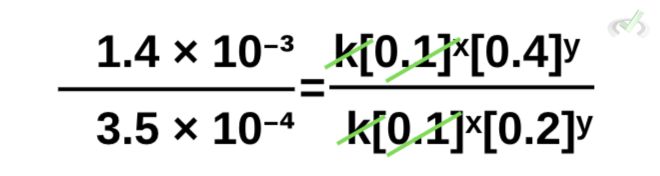
Rewriting the equation, we get:
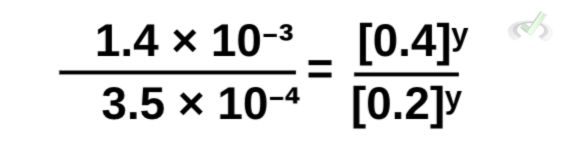
Simplifying the left side of the equation,
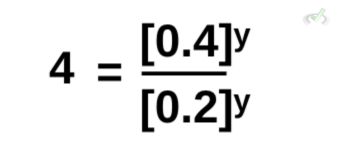
Similar to what we did earlier, the right side of the equation has y as an exponent. This is the same as having (0.4/0.2)สธ. We can then rewrite this as:
To get the value of y, we rewrite 4 so we can get the same base. Conveniently, 4 is equal to 2 squared. This effectively gives us the same base to get the exponent y. Thus, for the value of y, we get:
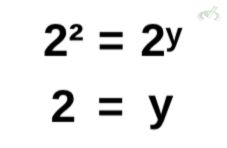
Here, we get the order of reaction for B as y = 2.
Step 2: Calculate the Rate Constant k
Our formula for the reaction rate now looks like this:
To calculate the rate constant, we can pick any trial and fill the equation with the data. This time, letโs use trial 2.
Filling in the formula, we get:
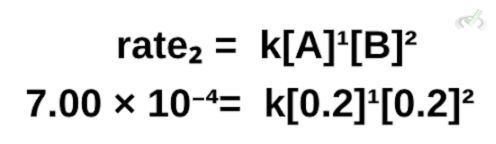
Simplifying this,
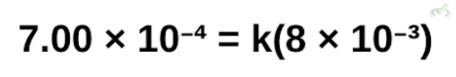
To get the value of k, we can simply divide both sides by 8*10โปยณ. Solving for this, we get the value for the rate constant k equal to 0.0875.
With this, we can find the rate of reaction for any concentration of reactants since we already have the orders of reaction for the reactants as well as the value of the rate constant k.
IV. Conclusion
The rate of reaction is an essential value in chemistry. It allows us to identify how fast a reaction takes place. We can find this using the rate law. One way of relating reaction rates is by equating the rate of reaction to the rate of disappearance of reactants or the rate of appearance of the products. Another way we can calculate this value is by explicitly using the equation and relating the rate of reaction using the order of reaction as indicated in the numerical coefficients in the balanced chemical equation. Lastly, we can use the rate law and experimental data of various trials of reaction.
V. Practice Questions
Use the data below to solve numbers 1 and 2.
Trial | [A] | [B] | [Initial Rate (M/s)] |
|---|---|---|---|
1 | 0.2 | 0.2 | 1.5 ร 10โปโด |
2 | 0.2 | 0.4 | 1.5 ร 10โปโด |
3 | 0.6 | 0.2 | 1.35 ร 10โปยณ |
Sample Practice Question 1
What is the order of the reaction of B?
A. 0
B. 1
C. 2
D. 3
Ans. A
Sample Practice Question 2
What is the value of the rate constant k?
A. 3.51 ร 10โปยณ
B. 3.15 ร 10โปยณ
C. 5.31 ร 10โปยณ
D. 1.35 ร 10โปยณ
Ans. D
To help you achieve your goal MCAT score, we take turns hosting these 
