Understanding how heat and entropy interact in chemical processes is essential for mastering general chemistry. These concepts help explain the energy changes and the disorder associated with chemical reactions.
I. Introduction to Heat and Entropy
Heat and entropy are fundamental concepts in thermodynamics, which study energy transformations in chemical reactions.
Heat
Heat (q) is the energy transferred between systems due to a temperature difference. It can be absorbed (endothermic) or released (exothermic) during a reaction. When a reaction is endothermic, it takes in heat from the surroundings, making them cooler. Conversely, exothermic reactions release heat, making the surroundings warmer.
Energy Diagram comparing exothermic and endothermic reactions:
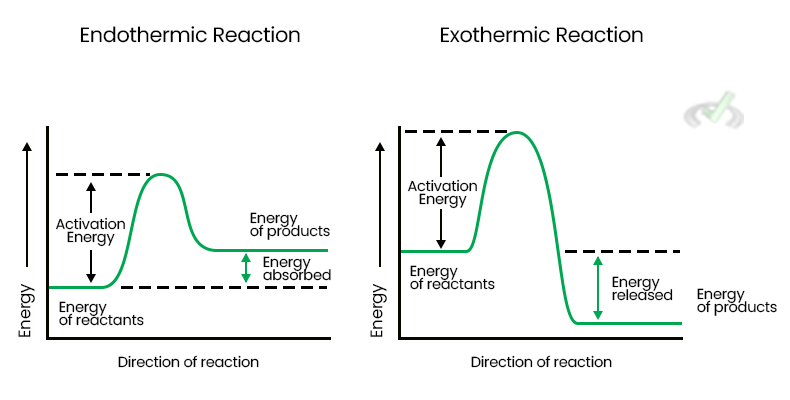
Entropy
Entropy (S) measures the disorder or randomness in a system. Greater disorder means higher entropy. For example, gas molecules have higher entropy than liquid molecules because they are more spread and disorganized.
II. Calculations Involving Heat
Understanding how to calculate heat changes in reactions helps predict how a system will respond to temperature changes.
Specific Heat Calculations
Specific heat is the amount of heat required to raise the temperature of 1 gram of a substance by 1°C. This property is important because it tells us how much energy is needed to change the temperature of a substance.
Example: Calculate the heat needed to raise the temperature of 100g of water from 25°C to 100°C. (Specific heat of water = 4.18 J/g°C)
Calorimeter Setup for measuring heat changes:
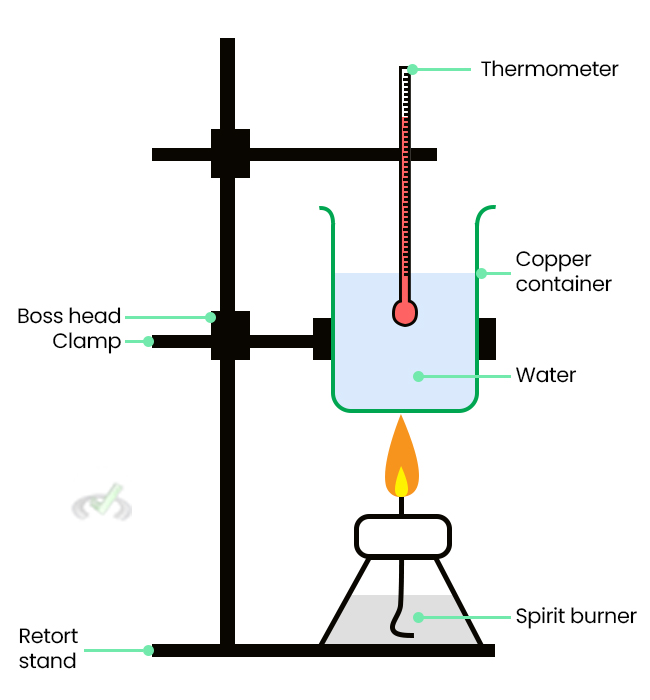
Heat of Reaction (Enthalpy Change)
The heat of reaction, or enthalpy change (ΔH), is the heat change at constant pressure. This is a key concept because it helps us understand how much energy is involved in making or breaking chemical bonds.
Equation:
△Σ = ΣHproducts – ΣHreactants
Example:
CH4 + 2O2 → CO2 + 2H2O
Given:
△Hf (CH4) = –74.8 kJ/mol
△Hf (CO2) = –393.5 kJ/mol
△Hf (H2O) = –241.8 kJ/mol
Solution:
△H = [(–393.5) + 2(–241.8)] – [(–74.8)]
△H = (–393.5 – 483.6) + 74.8
△H = –802.3 kJ/mol
III. Calculations Involving Entropy
Entropy Change (△S)
Equation:
△S = ΣSproducts – ΣSreactants
Given:
S(N2) = 191.5 j/mol K
S(H2) = 130.6 j/mol K
S(NH3) = 192.5 j/mol K
Solution:
△S = [2(192.5)] – [191.5 + 3(130.6)]
△S = 385 – (191.5 + 391.8)
△S = 385 – 583.3
△S = –198.3 j/mol K
Entropy changes in different states of matter:
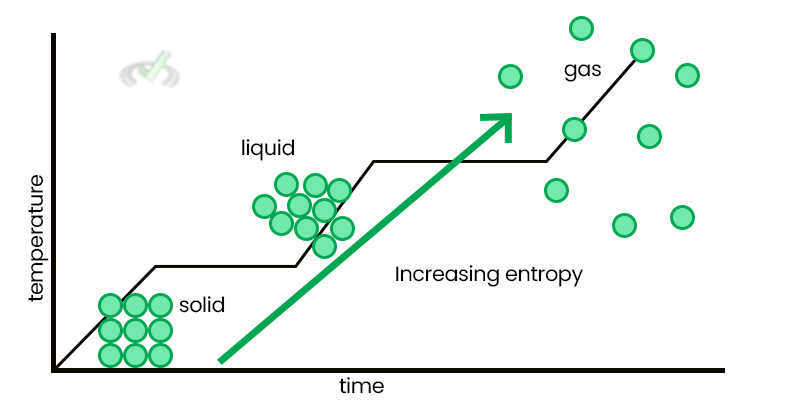
IV. Free Energy and Spontaneity
Free energy (G) combines enthalpy and entropy to predict the spontaneity of reactions. Gibbs Free Energy (ΔG) is particularly useful for this purpose.
Gibbs Free Energy (ΔG)
Equation:
△G = △H - T△S
△G < 0: Reaction is spontaneous
△G > 0: Reaction is non-spontaneous
△G = 0: Reaction is at equilibrium
Example: Calculate △G for the reaction at 298 K where △H = -802.3 kJ/mol and △S = -198.3 j/mol K.
Gibbs Free Energy Graph
Graphical illustration of Gibbs Free Energy versus reaction progress for spontaneous and non-spontaneous reactions.
V. Bridge/Overlap
Heat and entropy calculations connect to many broader topics in chemistry.
Thermochemistry
Thermochemistry involves the study of energy changes during chemical reactions and phase changes. Understanding heat and entropy is essential for analyzing reaction energetics.
Reaction Mechanisms
Knowledge of thermodynamics helps explain why certain reaction pathways are favored over others. Reactions tend to proceed towards lower free energy states.
Environmental Chemistry
Entropy and energy considerations are crucial in understanding environmental processes like pollution control and energy resource management. For instance, the breakdown of pollutants often involves changes in entropy.
Biochemical Pathways
Heat and entropy changes play a crucial role in biochemical pathways like glycolysis and the Krebs cycle. These pathways involve multiple steps in which cells convert and utilize energy.
Pharmaceutical Applications
Understanding the thermodynamics of drug binding in drug design can help develop more effective medications. Drugs that bind more efficiently to their targets typically lead to more successful treatments.
VI. Wrap-Up and Key Terms
To master heat and entropy calculations, keep these key terms in mind:
- Heat (q): Energy transfer due to temperature difference.
- Entropy (S): Measure of disorder.
- Enthalpy (ΔH): Heat change at constant pressure.
- Gibbs Free Energy (ΔG): Combines enthalpy and entropy to predict spontaneity.
VII. Practice Questions
Sample Practice Question 1
A reaction occurs in a closed system, absorbing 150 J of heat from its surroundings. If the specific heat capacity of the substance involved is 2.5 J/g°C and the mass is 50 g, how much will the temperature of the substance increase?
A. 0.3°C
B. 1.2°C
C. 2.4°C
D. 3.0°C
Ans. B
The heat absorbed by the substance (q) can be calculated using the formula: q=m⋅c⋅ΔTq=m⋅c⋅ΔTWhere:
- q=150 J
- m=50 g
- c=2.5 J/g°C
Rearranging to solve for the temperature change (ΔT): ΔT=qm⋅c=150 J50 g×2.5 J/g°C=1.2°C So, the temperature of the substance increases by 1.2°C.
Sample Practice Question 2
Which reactions are most likely spontaneous based on entropy changes alone?
A. Solid-to-liquid transition
B. Liquid-to-solid transition
C. Gas-to-liquid transition
D. Liquid to gas transition
Ans. D
Entropy (S) measures a system's disorder. A transition from a liquid to a gas involves a significant increase in entropy because gas molecules are much more disordered and spread out than liquid molecules. This increase in entropy makes the liquid-to-gas transition more likely to be spontaneous based on entropy considerations alone.
To help you achieve your goal MCAT score, we take turns hosting these 
