Fluids are substances that can flow. They include liquids and gases. Fluids are a fundamental part of our environment, found in everything from the water we drink to the air we breathe. Understanding them helps us explain many natural phenomena and engineering applications.
I. Basic Concepts
Understanding the basic concepts of fluids is essential for grasping more complex fluid dynamics. We will explore pressure, density, and buoyancy, which are foundational to studying fluids.
Pressure

Pressure is the force applied per unit area. Imagine pressing your hand on a table. The harder you press, the more pressure you apply.
In fluids, pressure is exerted equally in all directions at a given depth due to the fluid's incompressibility. The formula for pressure is:
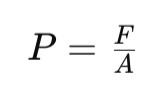
Where P is pressure, F is force, and A is area.
Density

Density is the mass of an object divided by its volume. For example, a rock is denser than water. That’s why rocks sink in water. The formula for density is:
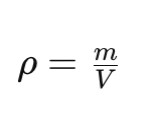
Where:
- ρ is density
- m is mass
- V is volume
Buoyancy
Buoyancy is the upward force that keeps objects afloat in a fluid. It’s responsible for the floating of boats in the water and the rising of helium balloons in the air due to the differences in density between the objects and the fluids. The buoyant force can be calculated using:
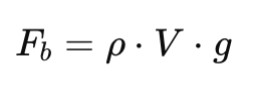
Where:
- Fb is the buoyant force
- ρ is the fluid density,
- V is the fluid displaced’s volume
- g is the acceleration due to gravity
II. Fluid Laws and Equations
Next, we will delve into the laws that govern how fluids behave under various conditions. These laws include Pascal’s Law, Archimedes’ Principle, and Bernoulli’s Principle, which are critical for understanding fluid dynamics.
Pascal’s Law
Pascal’s Law states that when pressure is applied to a fluid in a closed container, it is transmitted equally in all directions. The formula for Pascal's Law is:
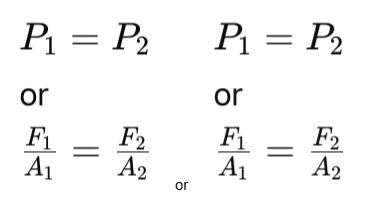
Where P1 and P2 are the pressures in different parts of the fluid. F1 and F2 are the forces. A1 and A2 are the areas of the pistons or surfaces.
For example, when you press the brakes in a car, the pressure applied to the brake pedal is transmitted equally through the brake fluid. This results in an equal force being applied to the brake pads at each wheel, which stops the car.
Archimedes’ Principle
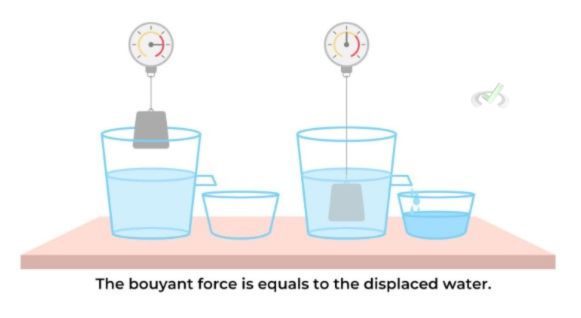
Archimedes’ Principle explains why objects float. It explains that when an object is submerged in a fluid, it encounters an upward force known as buoyancy, which is equivalent to the weight of the fluid it displaces.
For instance, putting a rubber duck in water pushes some water out of the way. The water pushes back with an equal force, making the duck float.
Bernoulli’s Principle
Bernoulli’s Principle states that in a moving fluid, as the speed of the fluid increases, its pressure also decreases. This principle explains why airplanes can fly.
The shape of the wings makes air move faster over the top of the wing, reducing pressure and creating lift. Bernoulli's equation is:
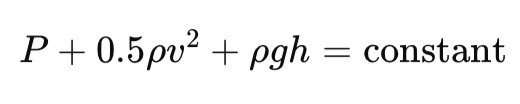
Where P is pressure, ρ is density, v is velocity, and h is height.
Equation of Continuity
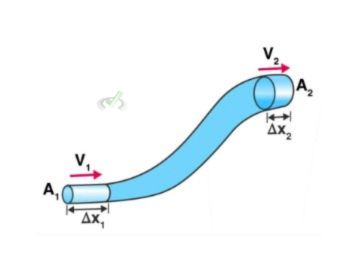
The Equation of Continuity is fundamental for understanding how fluids flow through different cross-sectional areas of a pipe or channel. This principle ensures that the mass flow rate remains constant along the path of the fluid flow.
It indicates that if a fluid speeds up, its cross-sectional area must decrease, and vice versa. The Equation of Continuity is expressed as:
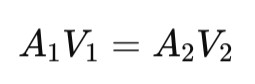
Where:
- A is the cross-sectional area
- V is the velocity of the fluid
Hydrostatic Pressure Equation
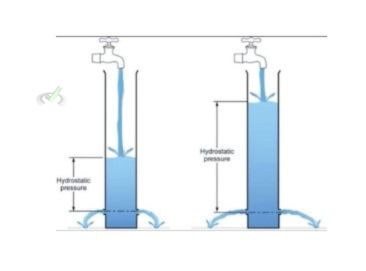
The Hydrostatic Pressure Equation is crucial in understanding how pressure increases with depth in a fluid at rest. This principle is essential for explaining why the pressure at the bottom of the ocean is much higher than at the surface. The Hydrostatic Pressure Equation is expressed as:
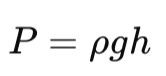
Where P is pressure, ρ is density, g is gravitational acceleration, and h is height.
III. Effects of Fluid Laws
Fluid laws are not just theoretical; they have practical applications in everyday life and technology. Understanding these effects can help us see the relevance of fluid dynamics in the real world.
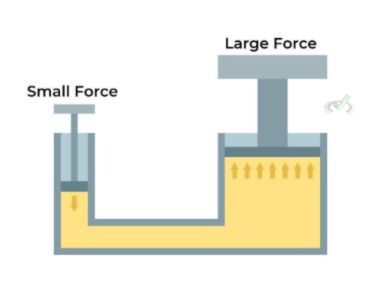
Hydraulic Lifts
Hydraulic lifts use Pascal’s Law to lift heavy loads. In these systems, a small force applied to a small-area piston is transmitted through a fluid to a larger-area piston.
Because the pressure is the same throughout the fluid, the force exerted by the larger piston is greater, allowing it to easily lift heavy objects. For example, car repair shops use hydraulic lifts to raise vehicles, making it easier to perform maintenance underneath them.
Boats and Submarines
Boats and submarines rely on Archimedes’ Principle for buoyancy control. A boat floats because it displaces a volume of water equal to its weight. The buoyant force, equal to the displaced water's weight, supports the boat.
Submarines adjust their buoyancy by taking in or expelling water from ballast tanks. When the submarine takes in water, it becomes heavier and sinks. When it expels water, it becomes lighter and rises.
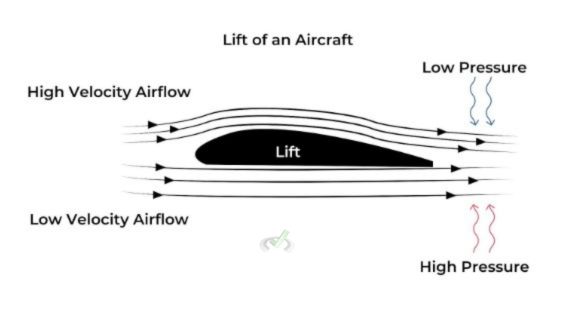
Airplane Wings and Sports Cars
Airplane wings and sports cars utilize Bernoulli’s Principle for lift and downforce. The shape of an airplane wing leads the air to move faster over the top surface than the bottom surface.
This creates a lower pressure on top and higher pressure on the bottom, generating a lift that allows the plane to fly. In sports cars, spoilers are designed to create downforce by reversing this principle, pressing the car down onto the road for better traction and stability at high speeds.
IV. Connecting Fluid Dynamics to Broader Concepts
Fluid dynamics connects with many other physics topics. Let's explore how these principles integrate with other areas of study.
Thermodynamics
In thermodynamics, understanding the behavior of gases is crucial for studying heat engines. The laws governing fluids help explain how engines convert heat into work.
Electromagnetism
In electromagnetism, fluid flow concepts help explain plasma dynamics. Plasma, often called the fourth state of matter, behaves like a fluid and is crucial in astrophysics and fusion energy research.
Cardiovascular and Respiratory Systems
In biology, fluid dynamics principles apply to blood flow in the cardiovascular system and airflow in the respiratory system. Understanding these principles is essential for medical studies and applications.
V. Wrap-Up and Key Terms
Understanding fluid laws, equations, and their effects helps us explain many natural and technological phenomena. These principles are foundational in physics and essential for various applications. Mastering them is important not only for academic success but also for practical problem-solving in everyday life.
Key Terms
- Pressure: Force per unit area.
- Density: Mass per unit volume.
- Buoyancy: The upward force exerted by a fluid on an object.
- Pascal’s Law: Pressure applied to a fluid is transmitted equally in all directions.
- Archimedes’ Principle: Buoyant force on an object is equal to the weight of the fluid displaced.
- Bernoulli’s Principle: In a moving fluid, an increase in speed results in a decrease in pressure.
VI. Practical Test
Sample Practice Question 1
A hydraulic lift is used to lift a car weighing 1500 kg. If the area of the small piston is 0.01 m² and the area of the large piston is 1 m², what is the force applied on the small piston to lift the car?
A. 150 N
B. 1500 N
C. 15000 N
D. 150000 N
Ans. C
Pascal's Law explains that when pressure is applied to a confined fluid, it is transmitted equally in all directions. Using the formula, we get:
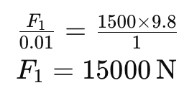
Sample Practice Question 2
Why do ships float on water while a small pebble sinks?
A. Ships are lighter than pebbles.
B. Ships are made of lighter material.
C. Ships displace a large amount of water, creating a buoyant force equal to their weight.
D. Ships are designed to float using Bernoulli’s Principle.
Ans. C
Archimedes' Principle states that an object submerged in a fluid experiences a buoyant force equal to the weight of the fluid it displaces. Ships are designed to displace a large volume of water, generating a buoyant force that keeps them afloat. On the other hand, a small pebble displaces a small amount of water and sinks due to its higher density.





 To help you achieve your goal MCAT score, we take turns hosting these
To help you achieve your goal MCAT score, we take turns hosting these