In the previous article, we talked about SI units. We learned that base units serve as the foundation of derived units and how we can simplify quantities without changing their value. This time, weโre going to use a concept that is highly underrated in math. Itโs a useful technique that if done correctly, will make solving problems easy without memorizing many formulas!
Dimensional analysis is a way of converting one unit to another. Itโs a neat way to visualize your math without thinking too hard about it.
I. The concept of dimensional analysis
Letโs look at our table of metric prefixes and notice a few things. The factor tells us how much of the base unit we have in relation to the prefix. Looking at 106, we see that itโs equivalent to a million of a unit. If weโre talking about 1000 mL (milliliter) of water, weโre also talking about 1 L (liter) of water.
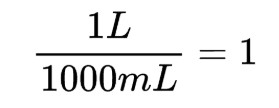
If we write it in fraction form, it is equal to one. One liter is the same as 1000 milliliters.
In dimensional analysis, we trick the number into thinking weโre not changing the value weโre converting by multiplying it by a value that is virtually equal to one. Unlike our previous method of conversion, where we move the decimal place into the number of places to convert it from one unit to another, dimensional analysis uses the idea that youโre multiplying the number you want to change by a value equal to one while changing the unit we want to convert.
For instance, letโs say we want to convert 12 kilometers into meters. Without looking at how many decimal places we have to move, we can simply do
Youโll notice that as we go through other examples of dimensional analysis, many units will cancel by multiplication, and the unit we want will always end up in the final answer. The beauty of dimensional analysis is that everything happens in one line of equations.
Letโs try simplifying 0.0000054 meters into micrometers.
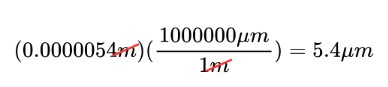
Since there is 1000000 ยตm (micrometers) in 1 m, we multiply this as a conversion factor to get our final value.
0.0000054 meters is equivalent to 5.4 ยตm.
II. Converting other values
Letโs try to find how many seconds there are in 2 days.
First, we know that there are 24 hours in 1 day. We can multiply 2 days by 24 hours/1 day to determine the number of hours in 2 days.
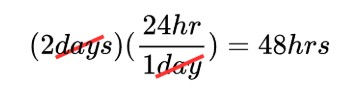
We also know there are 60 minutes in 1 hour and 60 seconds in one minute.
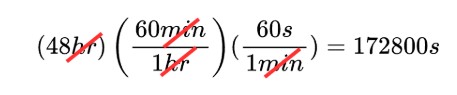
There are 172,800 seconds in 2 days.
There isnโt a strict way of doing dimensional analysis, but the basics of it go like this:
Step 1: Know the value
In the previous example, we were asked to know how many seconds there are in 2 days. Therefore, the time it takes to convert the value is 2 days.
Step 2: Write your conversion factors
We must list the conversion factors we will use to convert days into seconds. Itโs easy to start thinking of conversion factors from our existing value until we reach the unit we want.
1 day = 24 hours
1 hour = 60 minutes
1 minute = 60 seconds
Step 3: Set it up
In setting up our equation, we want to put our conversion factors as a fraction wherein we immediately cancel our initial value. In this case, we place 24 hours - 1 day immediately after 2 days to easily see that our value gets converted along the way.
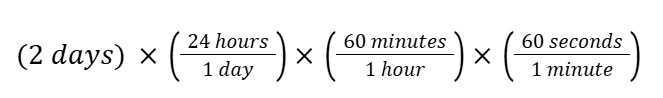
Step 4: Solve!
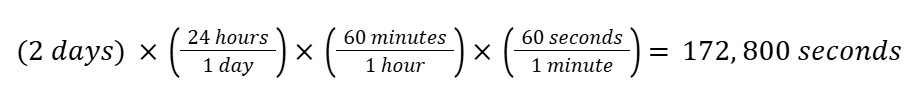
When we write our equation this way, we immediately see units canceled and clearly see how we end up with our desired unit.
III. More Examples
A. Converting from one system of unit to another
Dimensional analysis works for more than one system of units. We can convert from SI units to other systems of units as long as we know the conversion factors equivalent to the units we want to change.
Say we want to convert 35 feet into centimeters.
Step 1:
Our value is 35 feet, and we want to convert it into centimeters.
Step 2: Conversion factors
1 meter = 3.28 ft
1 meter = 100 cm
Step 3: Set up
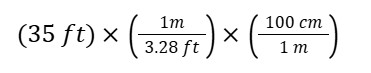
Step 4: Solve
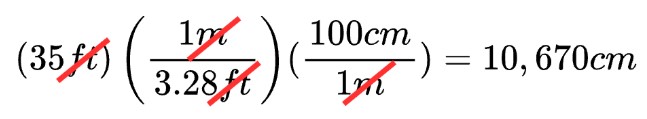
35 ft is equivalent to 10,670 cm
B. Converting quantities with exponents
We handle units with an exponent when converting quantities like area and volume. Solving for this is quite simple. Once we set up our line of equation, we raise the conversion factor to the power of the quantity weโre converting.
Letโs try to convert an area of 25m2to square feet.Step 1:
Our value is 25mยฒ
Step 2: Conversion factors
1 meter = 3.28 ft
Step 3: Set up
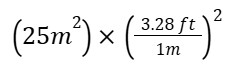
We raise our conversion factor to the same power as our original unit. Since the area is in square meters, our answer must also be in square feet. Otherwise, we wonโt be converting our area properly.
Step 4: Solve
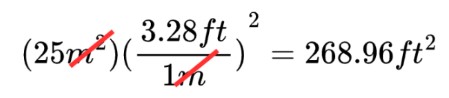
25 mยฒ is equivalent to 268.96 ftยฒ
C. Converting more than 2 units
The same principle applies to converting multiple units. For example, we might want to convert 16 miles per hour into meters per second.
Step 1:
We want to convert 16 mi/hr into m/s
Step 2: Conversion factors
1 mi = 1.6 km
1 km = 1000m
1 hr = 60 mins
1 min = 60 seconds
Step 3: Set up
Step 4: Solve
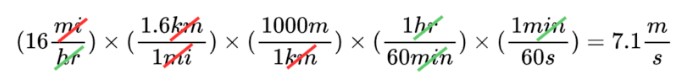
16 mi/hr is equivalent to 7.1 m/s
IV. Summary
Dimensional analysis is a great way to convert units from one unit to another. It solves the problem of resorting to multiple solutions, which almost always confuses anyone. Itโs a neat way of putting conversion into a line of equations where everything is laid out, and conversion can be seen every step. One important aspect of dimensional analysis is listing the relevant conversion factors you need for your value. Once everythingโs set and all the unnecessary units cancel, youโre left with an accurate conversion of your original value.
To help you achieve your goal MCAT score, we take turns hosting these 
