Units are complex because there are just too many of them, and there's even a fight over which system of units is the best. While we usually use miles and yards, the general convention that is more standard and understandable is the SI system. The SI system is the international system of units, the accepted measurement standard. The MCAT usually uses the SI unit, so we should go through this early.
I. Base Units
Base units are fundamental SI units that serve as the basis of derived quantities. These are simple and set to have a well-standardized way of measurement without considering other units such as inches to foot to yard and whatnot; SI units just make more sense and are easier to understand for most people, which you'll know as we go through our lessons.
You'll see in the table below the seven different base quantities. The SI system's base unit is second and not minutes or hours. Temperature is measured as kelvin. Having a universally accepted measurement system allows everyone to have the same measurement basis without worrying about how one country measures a specific quantity.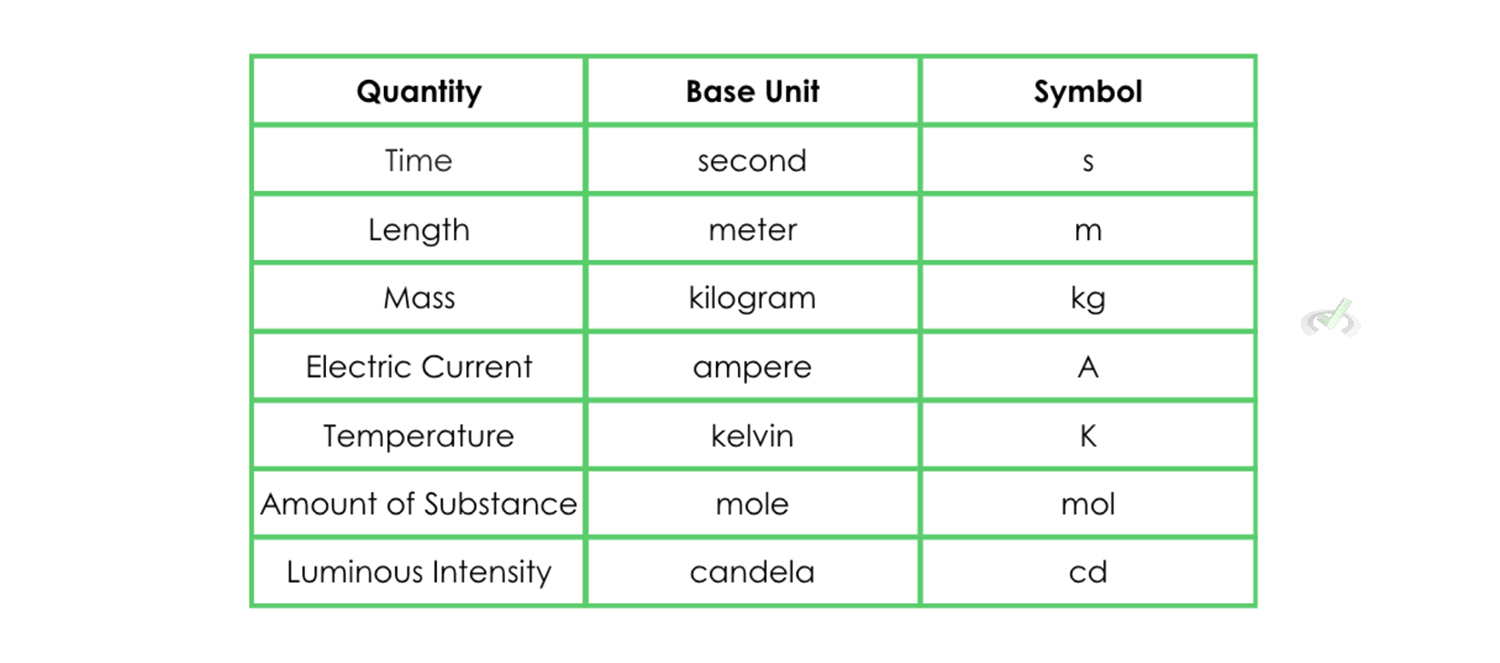
II. Derived Units
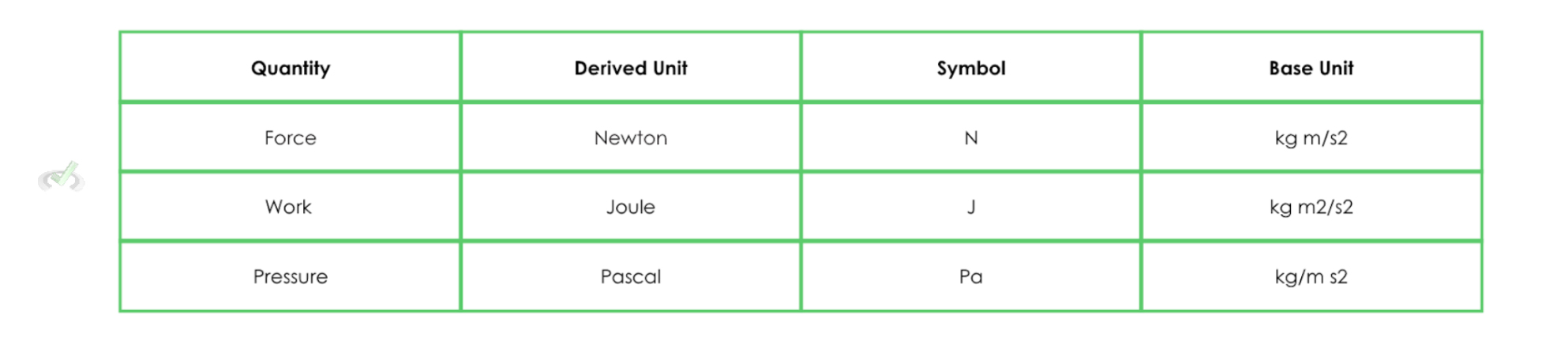
Derived units are quantities that are derived from base units, literally. It measures a wide range of properties without compromising accuracy and consistency from the base unit. Take work, for example.
The formula for work is
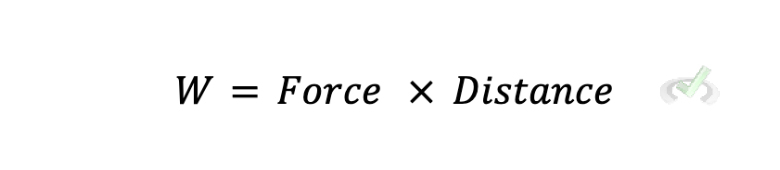
If we take the SI units of force and distance,
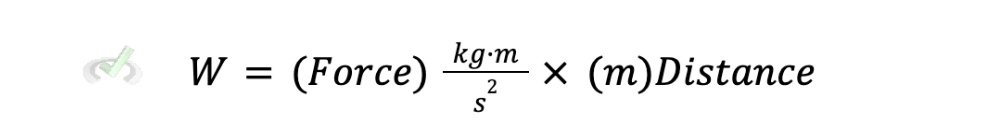
We should get the derived unit for work if we simplify these units.
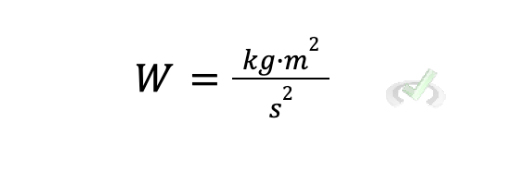
Work measures how much energy (Force) is used when one thing is moved over a distance. We can clearly see how these two measurements are considered and derived to form the SI unit for work. Similarly, force can be calculated by multiplying the mass (kg) by the acceleration of an object (ms2). When multiplied, we get a derived unit for force that is kgms2. Simply put, derived units use base units as a fundamental property to express their magnitude.
III. Metric Conversion
Metric conversion is a shorthand way of expressing the magnitude of the base unit. Things can get really confusing if we say that we must take 0.0012 L (liters) of medicine. A much neater way to put it is by saying we must take 1.2 mL (millimeters) of medicine. Note that 0.0012 L is just the same as 1.2 milliliters. We use the metric system to simplify the magnitude of the base unit without changing its value.
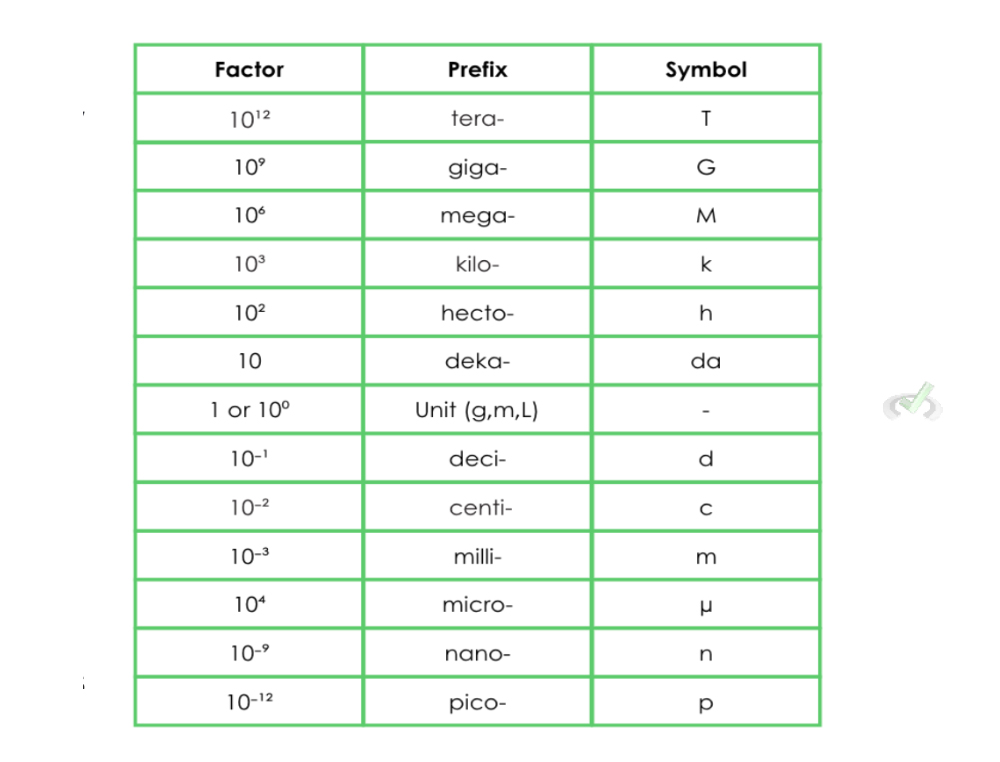
If we're asked about the diameter of the earth, it might be too complicated to say that the earth is approximately 12,700,000 meters in diameter. That's just too many numbers already. The table shows that 1 kilometer has 1000 (10³) meters. Therefore, we can say that the earth's diameter is around 12,700 kilometers by adding the prefix "kilo" to account for the 1000 meters that we counted as kilometers.
If we need to define how much storage we have on our phones, it's inconvenient to say that we have 256,000,000,000 bytes of storage. A much simpler way of putting it is just saying 256 GB (gigabytes). Since the prefix "giga" is 1,000,000,000 (10⁹) of the base unit, we can use it to say that we have 256 GB (256 of 10⁹ bytes).
Say we're defining the size of a cell that is 0.000001 meters. It's difficult to visualize because of the overwhelming number of zeros in front of it. A more standard way of defining cell size is in micrometers (μm) or microns that way, we can just say that a cell is approximately 1 micrometer/micron.
If you're still having a hard time, don't worry! Here's an example.
A. Example 1
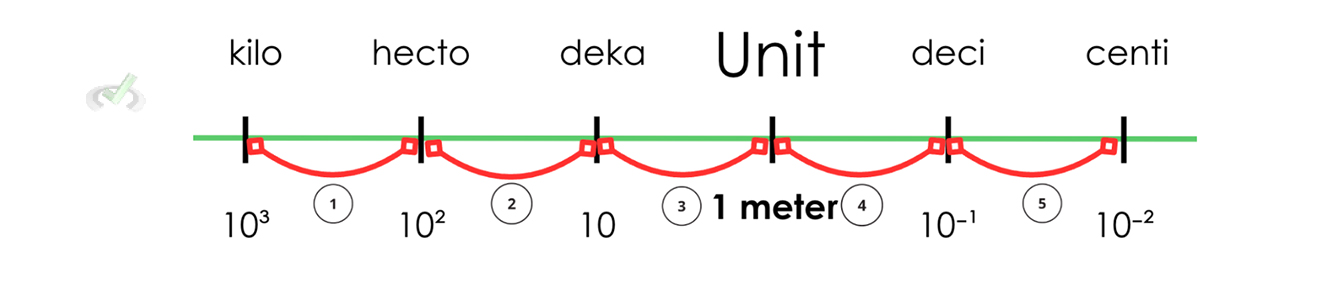
Say we want to convert 2 meters into kilometers. Using the guide below, we can visualize how "far" a kilometer is from the base unit.
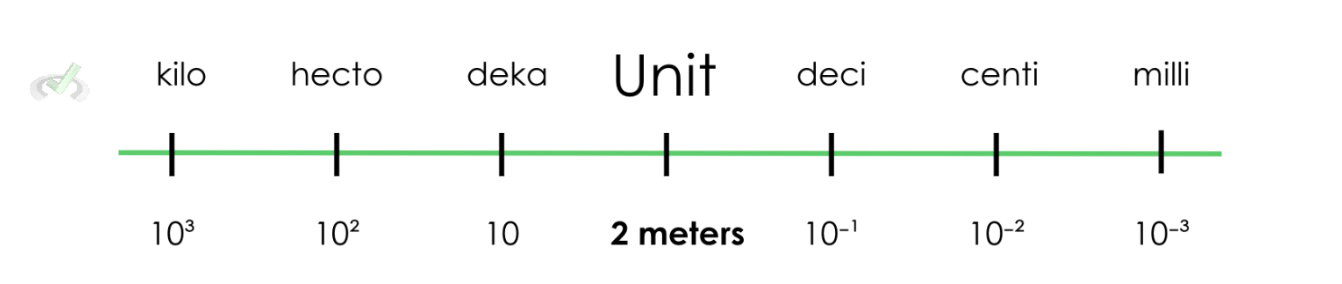
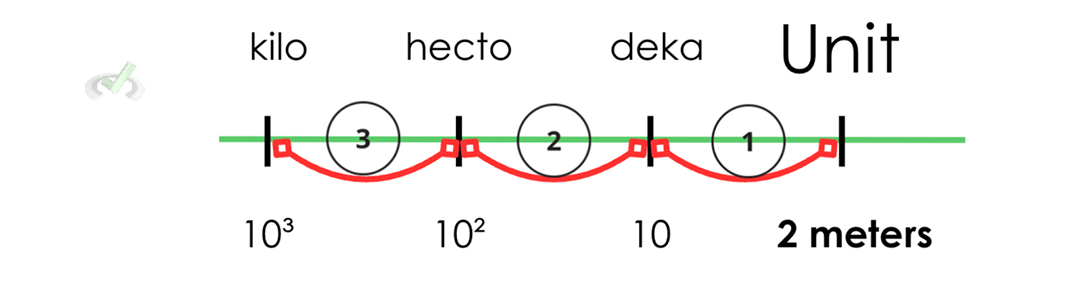
If we count how many "spaces" we have to get to kilometers, we see that we're moving 3 spaces from right (meter) to left (kilo) to move from our original unit to the unit we want.
Note that whole numbers have decimal points immediately after them.
To convert meters into kilometers, we must move the decimal point the same number of times as we did using the guide. Here, we moved three places to the left. If we move the decimal point three spaces to the left, we get:

Decimals always have zero before them if no whole number precedes them.
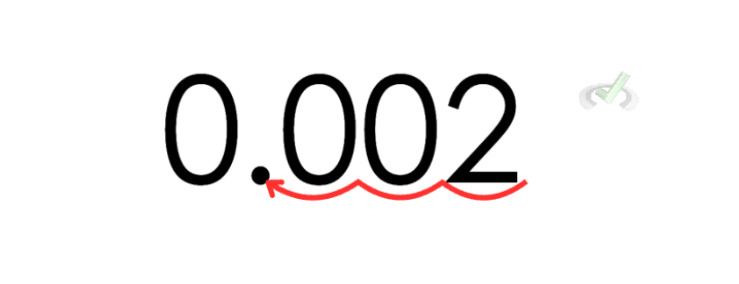
Thus, 2 meters is equivalent to 0.002 kilometers.
B. Example 2
Now let's say we want to know how many centimeters are 15 kilometers. Looking at our guide, we see that to move from kilometer to centimeter, we have to move 5 places from left (kilo) to right (centi).
Whole numbers have a decimal point immediately after it. If we move 5 places to the right in the same way we did in the last example, we get:

Since the decimal point is now at the end of a whole number, we can ignore it.
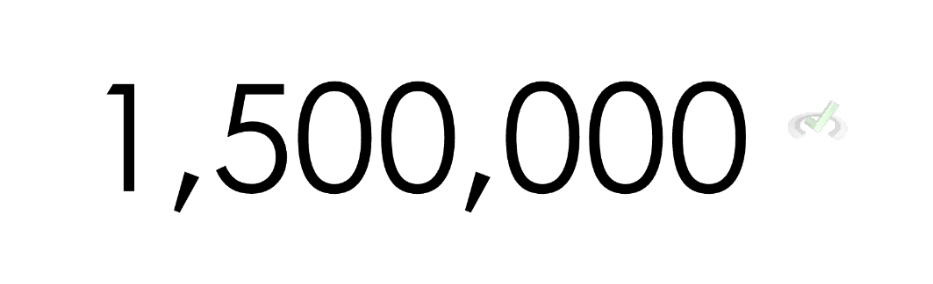
Therefore, 15 kilometers is equivalent to 1,500,000 centimeters.
C. Example 3
Without using our guide, we can use the exponents from the table. For instance, say we want to convert 75 kilograms to milligrams. From the table,

We can subtract these exponents to know the number of places we have to move the decimal point.
3-(-3)=6 (operation becomes positive when we subtract a negative)
Since we're moving from kilo to milli, we're moving six places to the right (a larger exponent to a smaller exponent).
Therefore, 75 kilometers is equivalent to 75,000,000 millimeters.IV. Summary
The SI Unit is a more standard way of expressing measurement. SI units have two types of units: base and derived. Base units are the foundation of much more complicated derived units. In contrast, derived units are units used in quantities that involve base units or a combination of based and derived units. Once we have our units set, we could encounter problems with how large or small our numbers might get. To simplify expressing the numerical value of units, we use prefixes to simplify the naming convention of specific quantities without changing their value. These prefixes correspond to the number of zeros before or after the decimal point, which changes how we write quantities.
V. Key Terms
- SI/Metric System - a system of measurement that is internationally recognized to provide a more cohesive way of measurement.
- Base Units - units that serve as the building block of derived units.
- Derived Units - units of measurement that use base units or a combination of derived and base units.
- Magnitude - the numerical value of a quantity.
- Prefix - a group of letters put in front of a root word to modify the root word’s meaning.





 To help you achieve your goal MCAT score, we take turns hosting these
To help you achieve your goal MCAT score, we take turns hosting these 




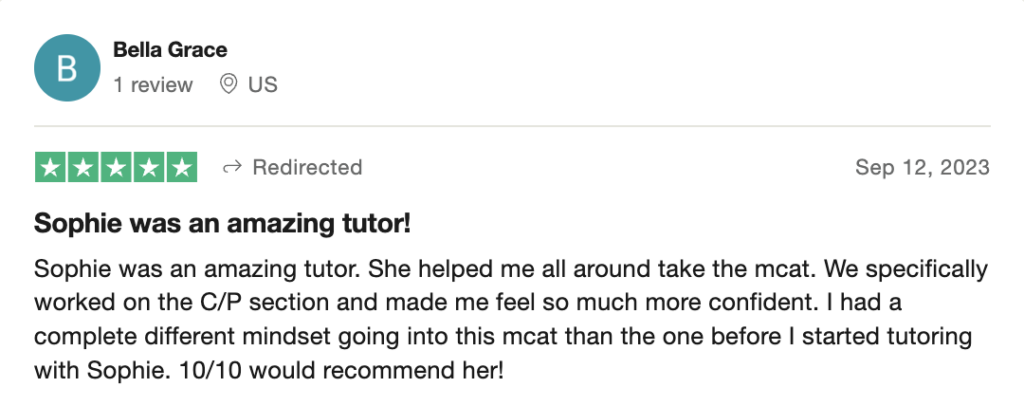

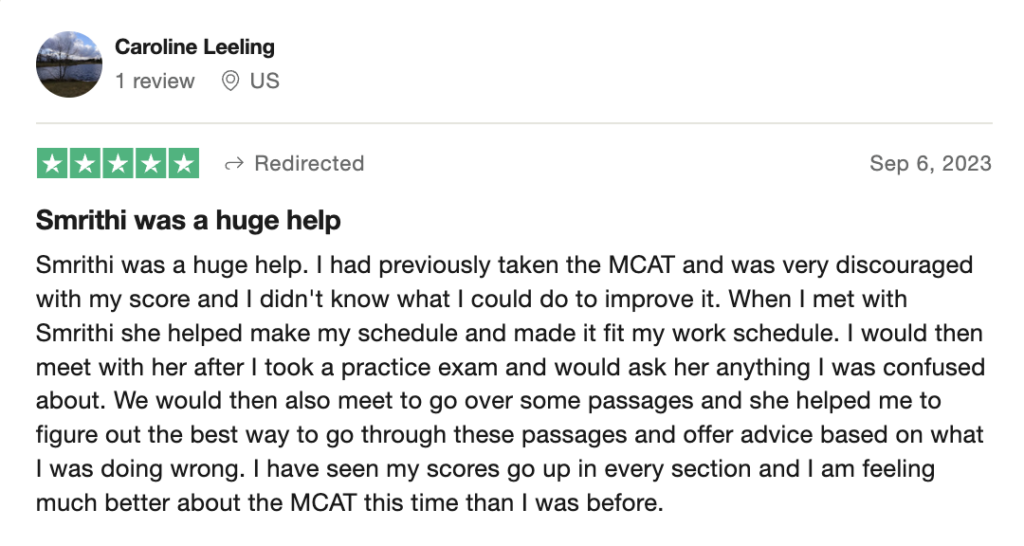





 reviews on TrustPilot
reviews on TrustPilot