Understanding the Work-Energy Theorem is essential in physics. It explains how work and energy are related and how energy changes form when work is done on an object. Let's explore this concept in detail.
I. Introduction to the Work-Energy Theorem
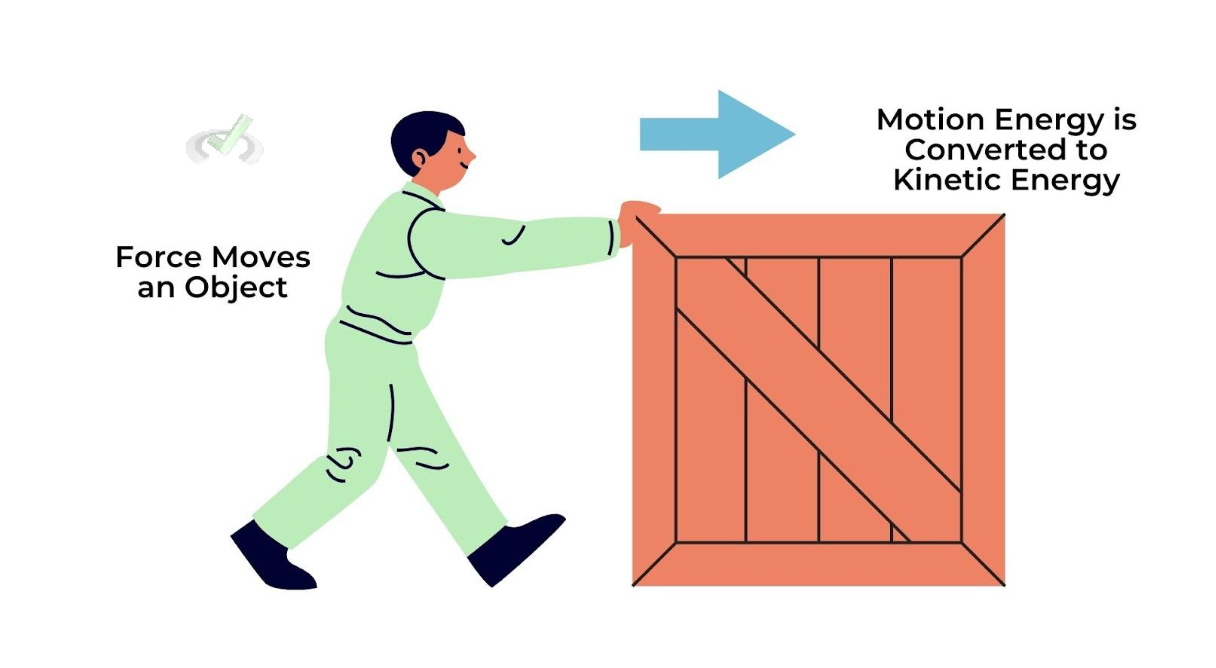
Imagine you are pushing a box across the room. As you exert force on the box, it moves, gaining speed and covering distance. This scenario exemplifies the Work-Energy Theorem in action.
According to Work-Energy Theorem, the work done on an object is equivalent to the change in its kinetic energy. In other words, when a force moves an object, the energy used to move it changes its motion energy, called kinetic energy (KE).
It is the type of energy an object has because of its motion. KE depends on both the mass of the object and its speed. The faster an object moves and the more massive it is, the greater its kinetic energy.
II. Calculating Work and Energy
Let's delve into how we calculate work and energy, focusing on their mathematical aspects and practical implications.
Work
To calculate work, you need to know the force applied and the distance over which it acts. If you push a sled with a force of 50 newtons over a distance of 10 meters, the work done is:
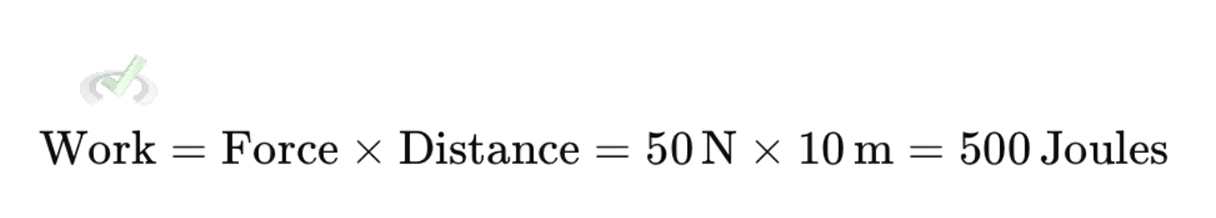
Here, joules (J) are the units of work and energy. One joule is the amount of work done when a force of one Newton moves an object one meter in the direction of the force.
Kinetic Energy
Kinetic energy, as mentioned, depends on the object's mass and its velocity (speed). The formula to calculate KE is:
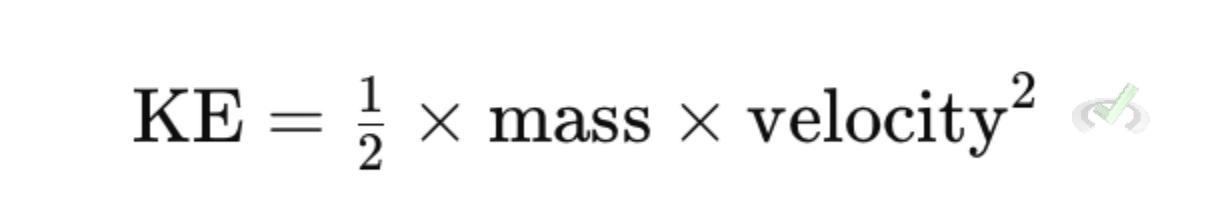
For example, if a sled has a mass of 20 kilograms and is moving at a velocity of 3 meters per second, its kinetic energy is:
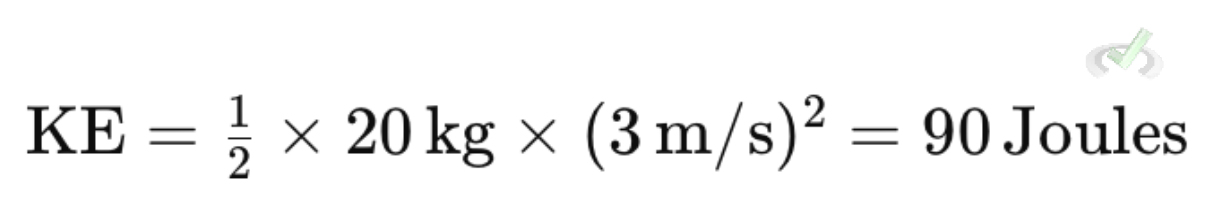
Work-Energy Theorem in Practice
When you push the sled and do 500 joules of work, this energy is transferred to the sled, increasing its kinetic energy. If the sled initially had 100 joules of kinetic energy, its final kinetic energy will be:
III. Connecting Work-Energy to Other Concepts
The Work-Energy Theorem is interconnected with various other concepts in physics. To deepen our understanding, let's briefly explore these connections.
Potential Energy
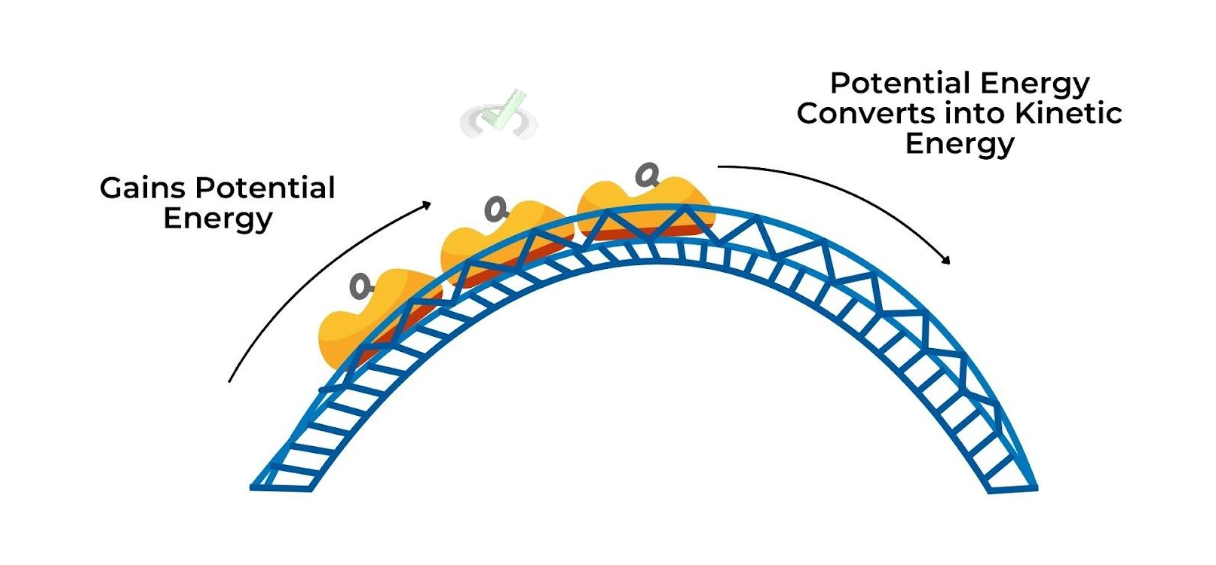
Potential energy is the type of energy stored in an object due to its position. When you lift an object, you work against gravity, increasing its potential energy. This energy can later convert to kinetic energy as the object falls.
For example, when a roller coaster car is lifted to the top of a hill, it gains potential energy. As it descends, this potential energy converts into kinetic energy.
Conservation of Energy
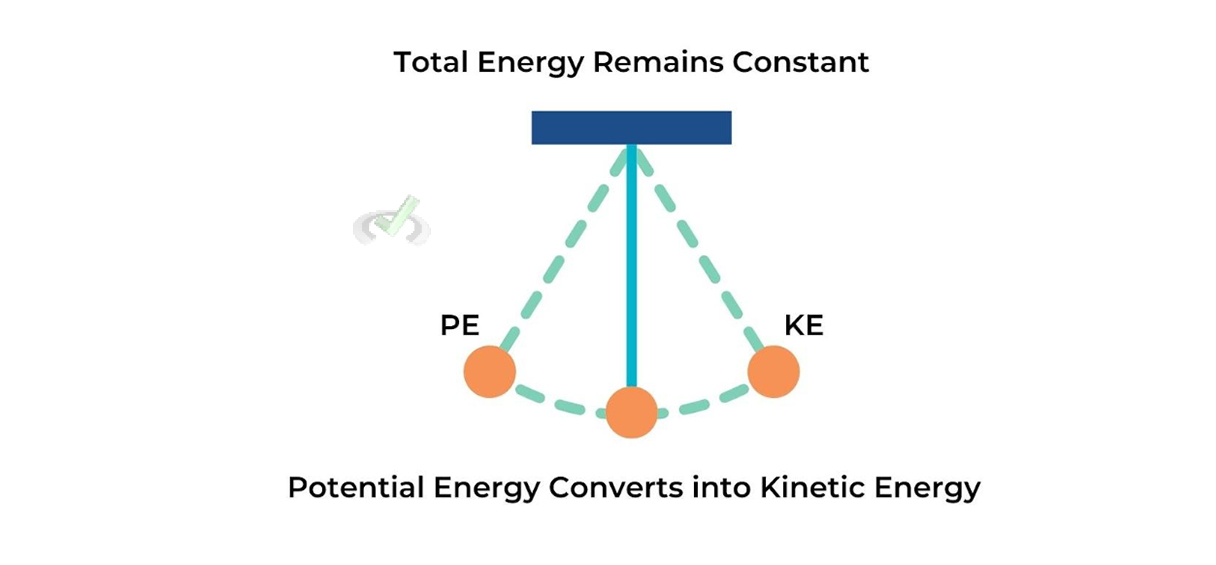
The conservation of energy principle explains that energy cannot be created or destroyed. It can only be transformed from one form to another. The Work-Energy Theorem specifically applies this principle, focusing on how work transforms into kinetic energy.
For instance, in a pendulum, the total energy remains constant as it swings, converting between potential energy at the highest and kinetic energy at the lowest points. Even though the energy changes form, the total amount of energy in the system does not change.
Power
Power is the rate at which work is done, or energy is transferred. It is calculated as work done divided by time taken (Power = Work/Time).
Understanding power helps us measure how quickly energy transformations occur. For example, a powerful engine can do more work in less time, resulting in faster car acceleration.
IV. Wrap-Up and Key Terms
Letโs review the key points we covered about the Work-Energy Theorem:
Key Terms
- Work: Force applied over a distance (W = F x d).
- Kinetic Energy: Energy of motion (KE=1/2รmassรvelocity2).
- Work-Energy Theorem: The work done on an object equals its change in kinetic energy.
- Potential Energy: Energy stored due to position.
- Conservation of Energy: Energy cannot be created or destroyed; it can only be transformed.
- Power: Rate of doing work (Power = Work/Time). One watt is equal to one joule per second.
V. Practice Questions
Sample Practice Question 1
What is the work done if a force of 30 newtons moves an object 5 meters?
A. 150 Joules
B. 50 Joules
C. 100 Joules
D. 200 Joules
Ans. A
Work is calculated by multiplying force by distance (W = F x d). Here, Work = 30 N x 5 m = 150 Joules.
Sample Practice Question 2
If a carโs kinetic energy increases by 400 joules after a certain amount of work is done, how much was done?
A. 200 Joules
B. 400 Joules
C. 600 Joules
D. 800 Joules
Ans. B
The Work-Energy Theorem explains that the work done on the car equals the change in its kinetic energy, which is 400 joules.
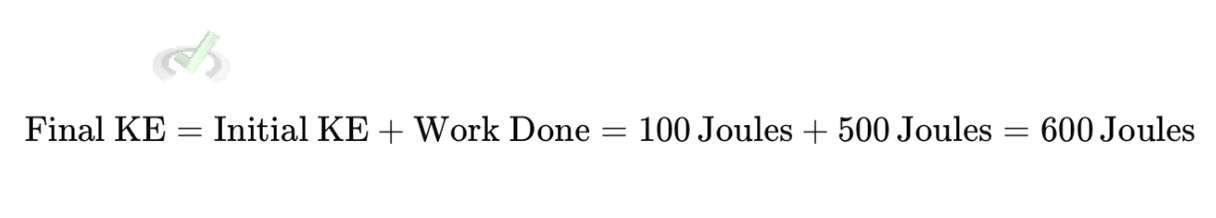
To help you achieve your goal MCAT score, we take turns hosting these 
