Scientific notation is a helpful way to rewrite large or small numbers. In our article on Units and Dimensions, we briefly discussed how to do this. We defined scientific notation as making big and small numbers bigger. This article will deeply dive into how we can do this accurately.
I. Scientific Notation Deconstructed
Let’s take a look at the following examples.
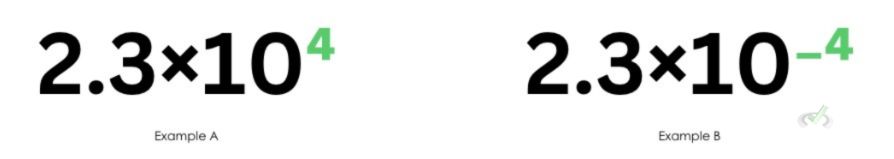
These numbers look similar, but they differ in value a lot. You might notice the key difference is the sign of the exponent. The first notation has a positive exponent, whereas the second notation has a negative exponent.

Positive exponents mean large numbers, and negative exponents mean smaller numbers. In expanding a scientific notation, note that we move the decimal point to the right when the exponent is positive. We have a positive exponent in example A, so we’ll move the decimal point to four spaces to the right.

Negative exponents mean small numbers. We move the decimal point to the left when expanding a scientific notation with a negative exponent. For example, in B, we’ll move the decimal point four spaces to the left since the original notation has a negative four (-4) as its exponent.

II. Writing in Scientific Notation
How about rewriting a number into scientific notation? We have to take four steps to rewrite a number into a scientific notation. For this one, let’s use examples C and D.

Step 1: Look at the value at hand
If the number has digits to the left of the decimal point, the decimal point moves to the left. If the number has digits to the right of the decimal point, the decimal point moves to the right.
Let’s take a look at examples C and D.

Example C is a whole number and has a decimal point after the one's place, so we will move the decimal point to the left. Example D has digits to the right of the decimal point, which means we’ll move the decimal point to the right.
Step 2: Move the decimal point
In scientific notation, we move the decimal point until it only has one non-zero number to its left.
Example C:
For example, A, whole numbers have a decimal point at the right of the one's place. We move the decimal point to the right so that only the number “5” is left to the left of the decimal point.

Example B:
For this example, we’ll move the decimal point to the left so that only one number remains to the left of our decimal point.

Step 3: Know your exponent
Count the number of places you moved to get the value of your exponent. If the exponent moves to the left or if you’re making a big number smaller, the exponent is positive. If the exponent moves to the right, making a small number bigger, the exponent shall be positive.
Example A:
Since the decimal point moved seven (7) places to the left, the exponent is positive seven (7).

Example B:
We moved the decimal point four (4) places to the right in this example. Therefore, our exponent is negative seven (-7).
Step 4: Write the scientific notation
Finally, you can write your scientific notation with 10 as the base. Remember that the base 10 represents the number of places you’re moving the decimal so as not to lose the number’s original value.

III. Operations with Scientific Notation
For most of the MCAT, solving numbers involving scientific notation will probably not be a problem, but if you encounter it, here’s a quick rundown on arithmetic with scientific notation.
A. Addition and Subtraction
The main rule about adding/subtracting numbers in scientific notation is that they must have the same exponent. If the exponents differ, rewrite one of the coefficients, so both have the same exponent. After converting these coefficients to have the same exponents, add/subtract the values before the power (×10ˣ). After adding/subtracting the coefficients, copy the common base and exponent.

B. Multiplication and Division
For multiplication and division, directly multiply/divide the coefficients. In multiplication, add the exponents and write them off as the exponent of the final answer, along with the product of the coefficients. During division, subtract the exponents of the divisor from the dividend. The difference will be the exponent of the final answer.

IV. Conclusion
Scientific notation allows us to simplify large and small numbers. Through this, we can visualize numbers simply. Calculations are also more simplified since we don’t consider all of the trailing zeroes that follow or precede the significant numbers. Proper notation is important, and one key trick is knowing that when we’re rewriting a large number, we move the decimal point to the left, which yields a positive exponent. For small numbers, we move the decimal point to the right, resulting in a negative exponent until only one digit precedes the decimal point–noting that all of these exponents have a base of 10. The rules of doing arithmetic are also pretty simple. Scientific notation allows us to handle and represent large and small numbers without the risk of inaccuracy.
V. Practice Questions
Sample Practice Question 1
In scientific notation, the value 0.0004302 can be rewritten as:
A. 43.02 x 10⁴
B. 4.32 x 10⁻⁵
C. 4.302 x 10⁻⁴
D. 4.302 x 10⁴
Ans. C
Sample Practice Question 2
Which of the following is not a product of 0.0013 and 4.35 x 10²
A. 5.655 x 10⁻¹
B. 5.655
C. 0.5655
D. 1131/2000
Ans. B






 To help you achieve your goal MCAT score, we take turns hosting these
To help you achieve your goal MCAT score, we take turns hosting these