Understanding the mathematics of vectors and scalars is crucial in physics. These concepts help us describe quantities that we encounter in the physical world. Letโs explore what vectors and scalars are and how they are used in physics.
I. Introduction to Vectors and Scalars
Imagine you are pushing a cart. The force you apply has a direction and a magnitude (how hard you push). This force is a vector. Now, think about the temperature in a room. The temperature has only a magnitude (how hot or cold it is), with no direction. This is a scalar.
- Vectors are quantities that have both magnitude and direction.
- Scalars are quantities that have only magnitude.
Understanding these concepts helps us describe physical phenomena more precisely. The direction of a vector tells us where the quantity is acting, while the magnitude tells us how much of it there is.
II. Scalars
Scalars are the simpler of the two types of quantities. A single value describes them and has no direction.
Examples of Scalars
Importance of Scalars
Scalars are essential in everyday measurements. They simplify many calculations and help us understand basic physical quantities.
For example, knowing the temperature helps us decide what to wear while knowing the time helps us manage our daily activities. Scalars are easy to work with because they only require one value.
III. Vectors
Vectors are more complex than scalars because they include direction as well as magnitude. Vectors are often represented by arrows. The length of the arrow represents the magnitude. Meanwhile, the direction of the arrow shows the direction of the vector.
Mathematically, vectors can be explained using coordinates. For example, a vector in 2D space can be written as (x,y)(x,y). This means the vector has a component xx in the horizontal direction and a component yy in the vertical direction.
Examples of Vectors
Operations with Vectors
Vector Components
Breaking down a vector into its components helps in calculations. A vector in 2D can be written as , where Vx and Vy are the components along the x and y axes, respectively. These components can be used to find the length (magnitude) and direction of the vector.
The magnitude of the vector can be solved using the Pythagorean theorem:
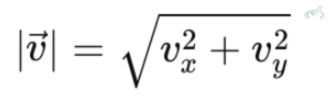
Dot Product and Cross Product
IV. Properties and Uses of Vectors and Scalars
Understanding the properties and uses of vectors and scalars allows us to solve various physics problems.
Key Properties of Scalars
- Additive Property: Scalars can be added together to get a new scalar. For example, adding temperatures.
- Multiplicative Property: Scalars can be multiplied to get a new scalar. For example, multiplying mass by acceleration to get force.
Key Properties of Vectors
- Direction and Magnitude: Vectors must include both elements.
- Vector Addition: The sum of two vectors depends on both their magnitudes and directions. This is crucial for understanding forces acting on an object.
V. Applications in Physics
Vectors and scalars are used extensively in physics to describe various phenomena.
VI. Connecting Vectors and Scalars to Complex Concepts
Understanding vectors and scalars is fundamental for more advanced topics in physics. For example:
Vector Fields
Vector fields describe how vectors change in space. Each point in space is associated with a vector. This concept is crucial in understanding various physical phenomena.
For instance, in a gravitational field, the vector at each point indicates the direction and magnitude of the gravitational force experienced by a mass placed at that point. The Earth's gravitational field can be represented by vectors pointing towards the center of the Earth, with their lengths proportional to the strength of the gravitational pull.
Electric and Magnetic Field
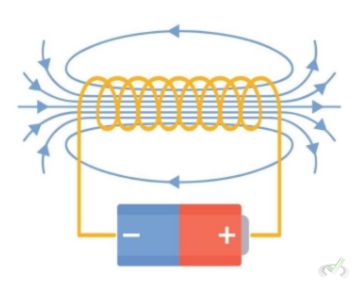
Both electric and magnetic fields are known vector fields that describe the forces experienced by charged particles. These fields are central to the study of electromagnetism. An electric field around a charged object can be represented by vectors pointing away from a positive charge or toward a negative charge.
The vectors' magnitude indicates the electric force's strength at different points in space. Similarly, a magnetic field around a magnet can be visualized with vectors showing the magnetic force's direction and strength.
The field lines around a bar magnet form closed loops. It starts from the north pole and ends at the south pole.
Quantum Mechanics
Quantum mechanics uses vectors, specifically state vectors, to describe the state of a quantum system. These vectors exist in a complex vector space called Hilbert space. In quantum mechanics, the state of a particle, such as an electron, is described by a state vector.
This vector contains all the information about the particle's properties, such as position, momentum, and spin. Understanding how these vectors change over time helps physicists predict the behavior of particles at the quantum level.
VII. Wrap-Up and Key Terms
Letโs review the key points we covered about vectors and scalars:
- Scalars: Quantities with only magnitude (e.g., temperature, speed).
- Vectors: Quantities with both magnitude and direction (e.g., displacement, force).
- Vector Addition: Combining vectors to get a resultant vector.
- Vector Components: Breaking vectors into parts along coordinate axes.
- Dot Product and Cross Product: Operations involving vectors that produce different results.
VIII. Practice Questions
Sample Practice Question 1
A car travels 100 meters north and then 100 meters east. What is the car's total displacement?
A. 200 meters
B. 100 meters north
C. 100 meters east
D. 141 meters northeast
Ans. D
To find the total displacement, we use the Pythagorean theorem. The displacement vectors form a right triangle, with the legs being 100 meters north and 100 meters east. The hypotenuse, which represents the total displacement, is calculated as:
Sample Practice Question 2
If a force of 20 Newtons is applied to an object in the east direction and another force of 15 Newtons is applied in the north direction, what is the magnitude of the resultant force?
A. 5 Newtons
B. 25 Newtons
C. 35 Newtons
D. 25 Newtons
Ans. D
The resultant force can be found by treating the forces as vectors and using the Pythagorean theorem. The forces form a right triangle, with the legs being 20 Newtons east and 15 Newtons north. The hypotenuse, which represents the resultant force, is calculated as:
To help you achieve your goal MCAT score, we take turns hosting these 
